Physics Lesson 16.6.2 - Ampere's Law

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 1 Votes ]

Welcome to our Physics lesson on Ampere's Law, this is the second lesson of our suite of physics lessons covering the topic of Ampere's Law, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.

Ampere's Law

In the tutorial 14.6 "Electric Flux - Gauss Law", we explained that the net outward normal electric flux through any closed surface is proportional to the total electric charge enclosed within that closed surface. For example, the net outward electric flux through a charged sphere is

Φ = E ∙ A
= 1/4πϵ₀ ∙ Q/R² ∙ 4πR²
= Q/ϵ₀

We can use the integral method to find the same result. Thus, for a small segment dA of the sphere, we have

dΦ = E ∙ dA

The total flux through the entire surface A is calculated by taking the integral of the above expression. We have:

Φ = ∫d Φ
= ∫E ∙ dA
= E ∙ A
= 1/4πϵ₀ ∙ Q/R² ∙ 4πR²
= Q/ϵ₀

As you see, the result obtained is the same for both methods used.

Similarly, we can find the net magnetic field due to any distribution of currents by first considering the differential magnetic field dB⃗. The magnitude of the elementary magnetic field produced by a current-length element idL⃗ at the given point P, which is at a distance r from the given current element, is (the scalar version):

dB = μ₀/4n ∙ idL ∙ sinθ/r²

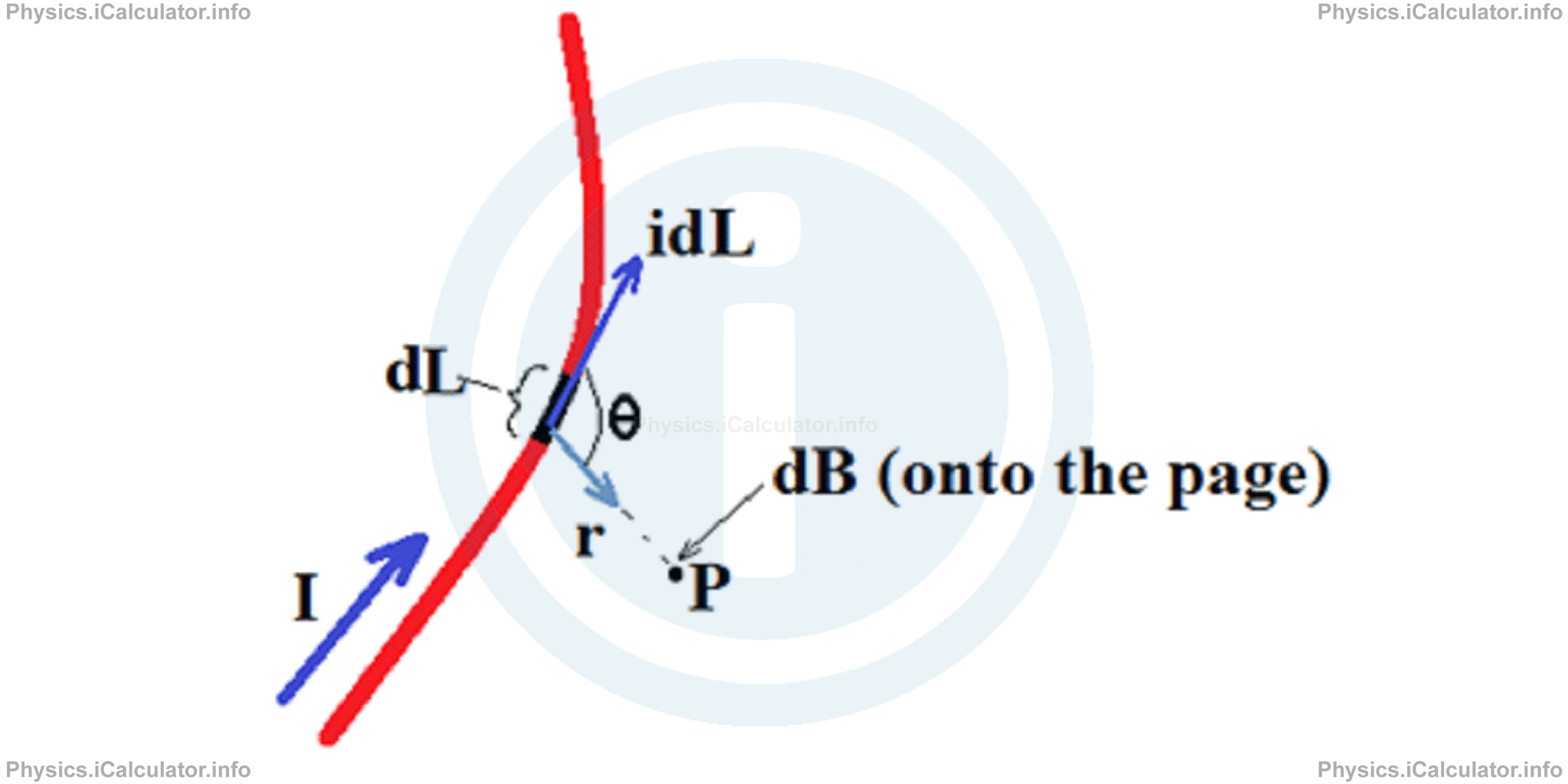
Physics Tutorials: This image provides visual information for the physics tutorial Ampere's Law

The above formula is known as the Biot-Savart Law. If the current distribution has some symmetry, we can integrate the above expression to obtain a simpler expression for the magnetic field. Thus, after making a few arrangements in the integral, we have

∫B dL = μ₀ ∙ i

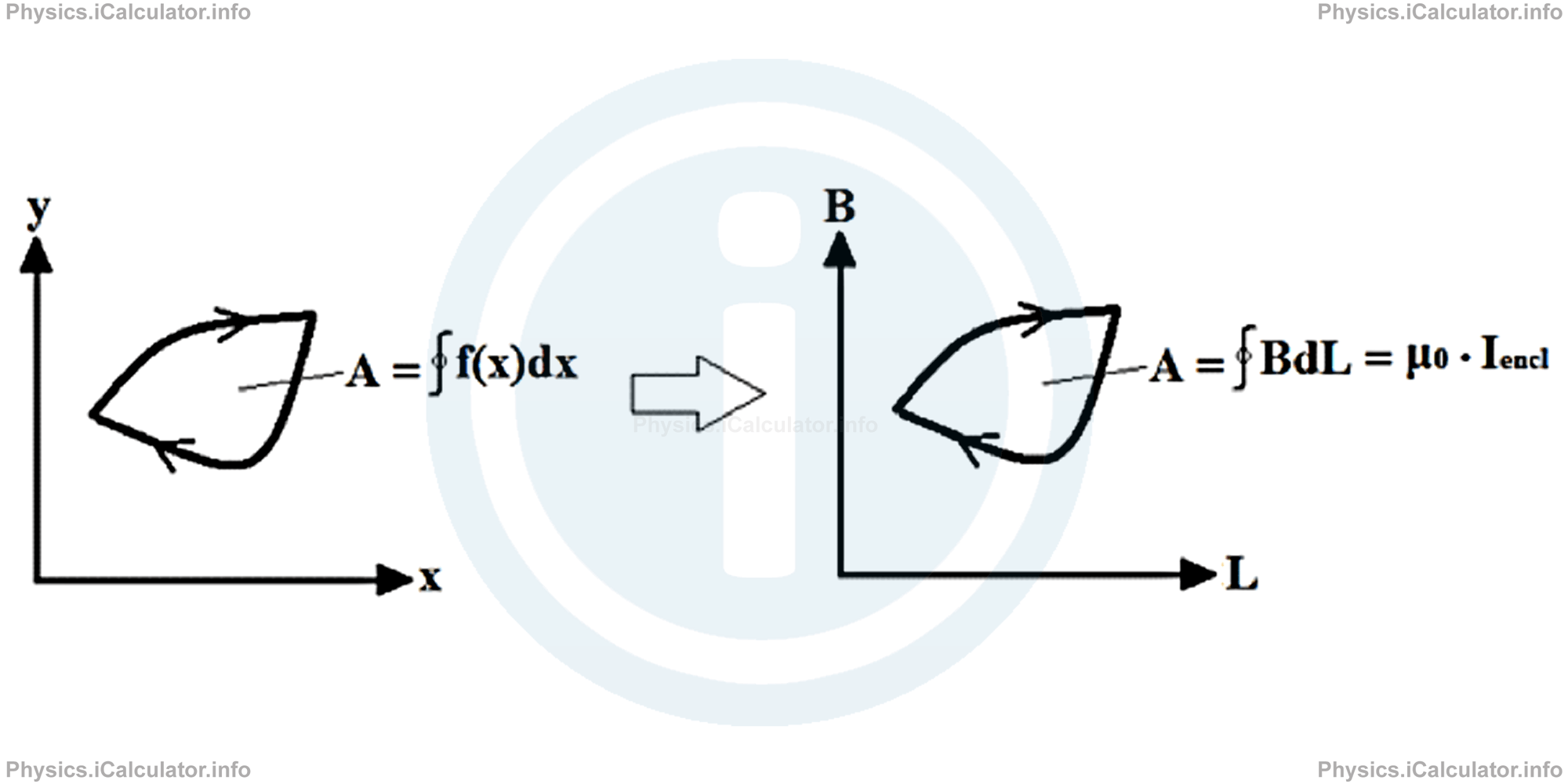
The above expression is known as the Ampere's Law and it is especially useful when considering the current flowing through a closed loop. In such cases, we can write:

∮B dL = μ₀ ∙ i_encl

By definition, Ampere's Law states that for any closed loop path, the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability of free space times the electric current enclosed in the loop.

The circle in the symbol of integral shows that it is the integral of a closed path (loop). Geometrically, it represents the area bordered by the graph only, not by the horizontal axis as in normal integrals, as shown in the figure.

Any closed loop as those discussed above is known as Amperian loop. The figure below shows an Amperian loop, which encircles two current carrying wires but excludes a third one. The directions of currents are shown through the known symbols ⊗ and ⨀.

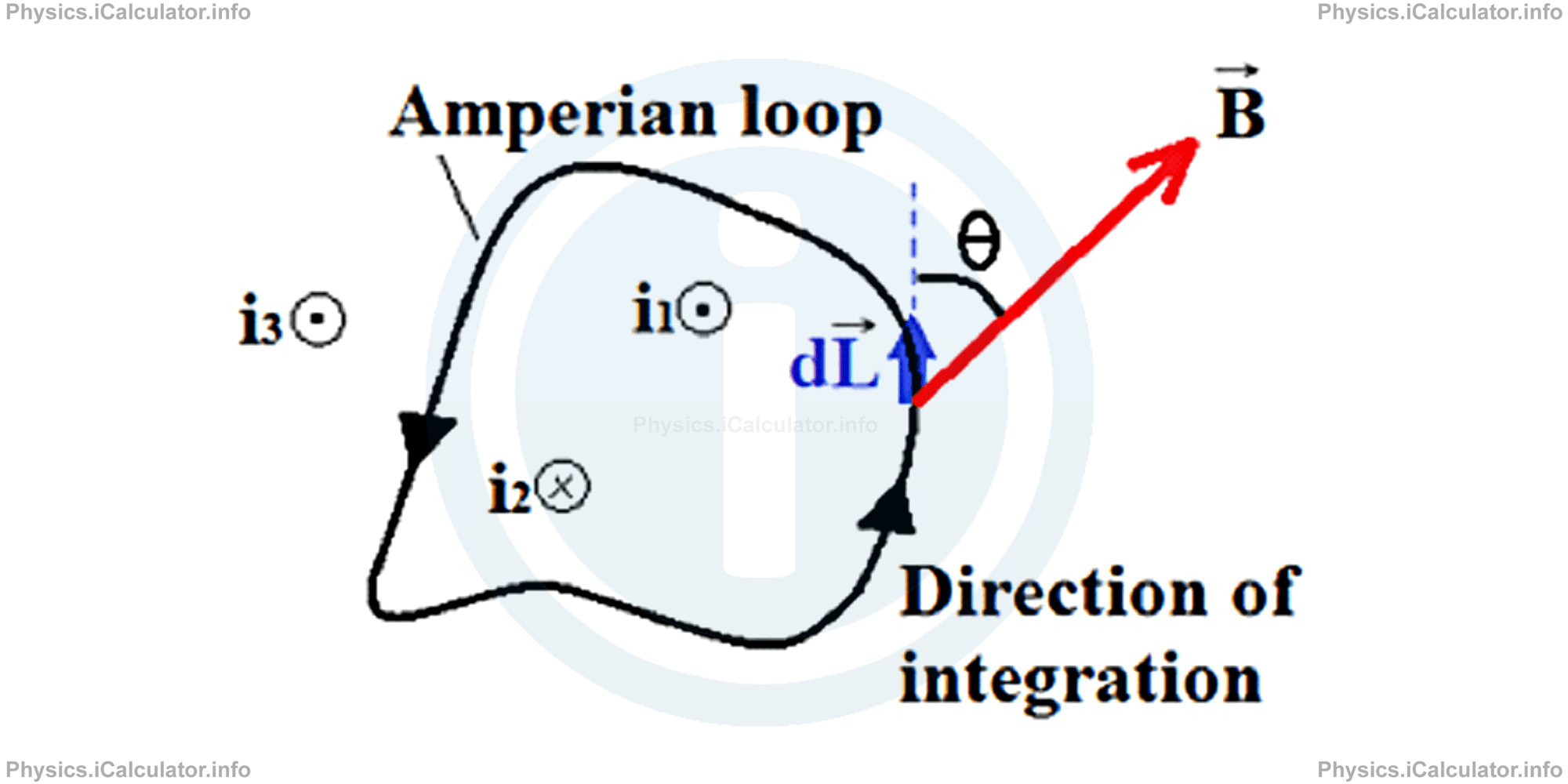
The direction of the currents is important to determine the current signs in the final formula after integration. For this purpose, we use the curled right hand rule in which the four fingers are placed in the direction of integration and the outstretched thumb shows the direction of a positive current. If the current is in the negative direction, it is taken as negative. As for the direction of magnetic field B, regardless its direction, it is generally assumed in the direction of integration for simplicity. This means it is not necessary to know the direction of magnetic field prior to integration.

For example, in the figure above, i₁ is positive as it is out of page and i₂ is negative (onto the page). Also, we have introduced an angle θ in the figure as the direction of magnetic field B is not exactly the same as that of the loop element dL in the given position. Hence, Ampere's law in vector form becomes

∮B⃗ dL⃗ = ∮B⋅cos⁡θ dL
= μ₀ ∙ i_encl

It is obvious that the expression B⃗dL⃗ inside the integral represents the scalar product of an elementary element dL of an Amperian loop and the magnetic field B in that position, which is tangent to the element dL. This means the value of integral represents the sum of all such products around the entire loop.

In our figure, the net current is

i_net = i₁ - i₂

Therefore, using Ampere's law for these two currents we obtain:

∮B⃗ dL⃗ = ∮B⋅cos⁡θ dL
= μ₀ ∙ i_encl
= μ₀ ∙ (i₁ - i₂)

For example, the value of integral above if i₁ = 5A and i₂ = 3 A is

∮B⃗ dL⃗ = μ₀ ∙ (i₁ - i₂ )
= 4π × 10^-7 N/A² ∙ (5A - 3A)
= 8π × 10^-7 N/A

Now, let's consider a couple of examples in which we can apply simple integration techniques to find what we are missing.

You have reached the end of Physics lesson 16.6.2 Ampere's Law. There are 5 lessons in this physics tutorial covering Ampere's Law, you can access all the lessons from this tutorial below.

More Ampere's Law Lessons and Learning Resources

Magnetism Learning Material
Tutorial ID	Physics Tutorial Title	Revision Notes	Revision Questions
16.6	Ampere's Law
Lesson ID	Physics Lesson Title	Lesson	Video Lesson
16.6.1	Useful Mathematical Background: Integral of a function - Geometrical approach
16.6.2	Ampere's Law
16.6.3	Magnetic Field Outside a Long Straight Wire with Current
16.6.4	Magnetic Field Inside a Long Straight Wire with Current
16.6.5	Ampere's Law Applied in Solenoids and Toroids

Whats next?

Enjoy the "Ampere's Law" physics lesson? People who liked the "Ampere's Law lesson found the following resources useful:

Definition Feedback. Helps other - Leave a rating for this definition (see below)
Magnetism Physics tutorial: Ampere's Law. Read the Ampere's Law physics tutorial and build your physics knowledge of Magnetism
Magnetism Revision Notes: Ampere's Law. Print the notes so you can revise the key points covered in the physics tutorial for Ampere's Law
Magnetism Practice Questions: Ampere's Law. Test and improve your knowledge of Ampere's Law with example questins and answers
Check your calculations for Magnetism questions with our excellent Magnetism calculators which contain full equations and calculations clearly displayed line by line. See the Magnetism Calculators by iCalculator™ below.
Continuing learning magnetism - read our next physics tutorial: Faraday's Law of Induction

Help others Learning Physics just like you