Menu
Physics Lesson 15.1.2 - Charge Density and Current Density. Why are they Different?
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Charge Density and Current Density. Why are they Different?, this is the second lesson of our suite of physics lessons covering the topic of Electric Current. Current Density, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Charge Density and Current Density. Why are they Different?
Let's consider again the example with the two containers discussed in the previous paragraph. We assume the density of flowing material (water) and that of the surrounding environment as equal in both containers when conclude that the flow will stop when water reaches the same level in both containers. However, if the container on the right has a higher air density than the container on the left, the equilibrium is settled when water is not at the same level in both containers (remember the effects of capillary action and air pressure explained earlier on the liquid flow).
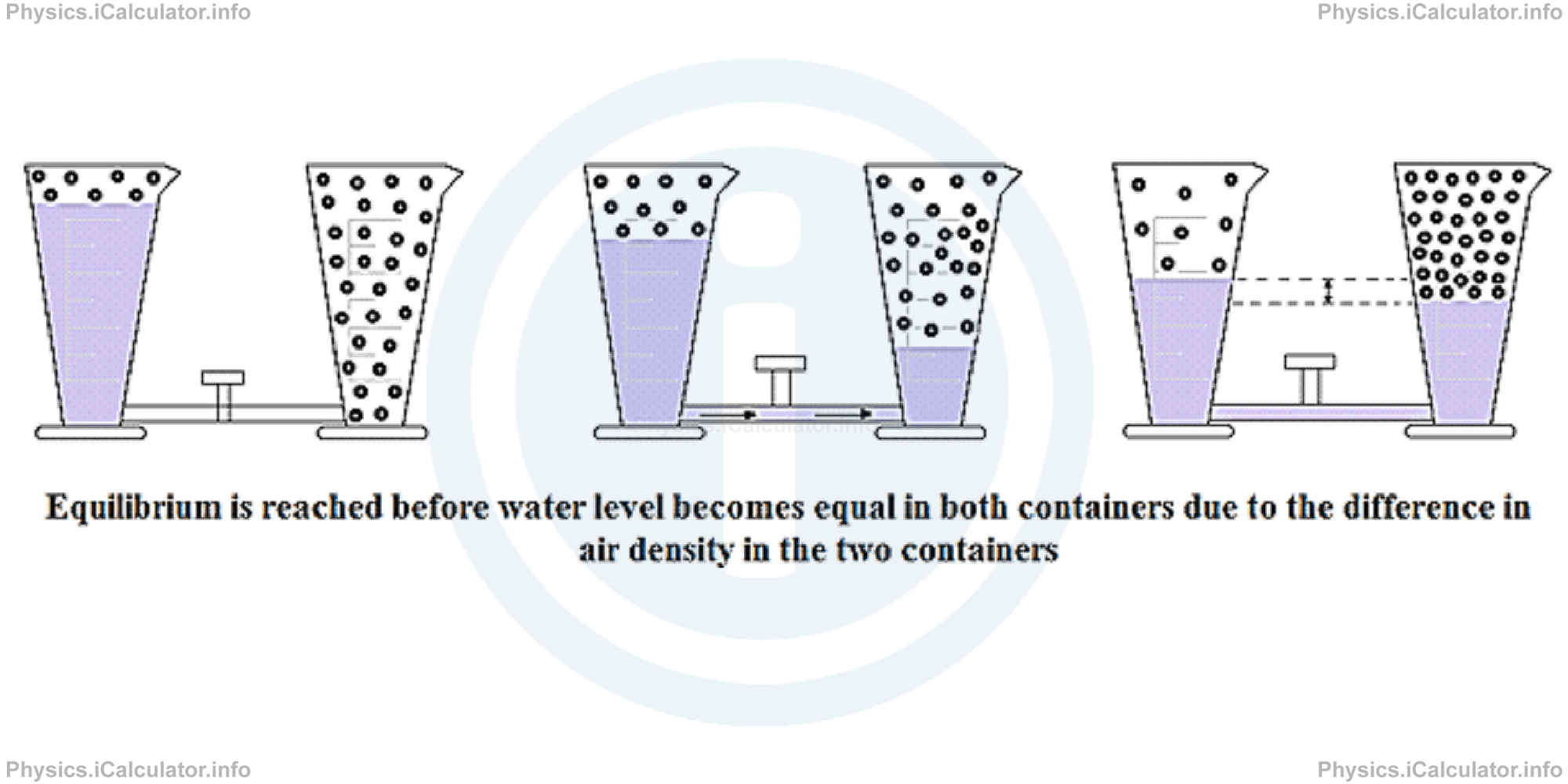
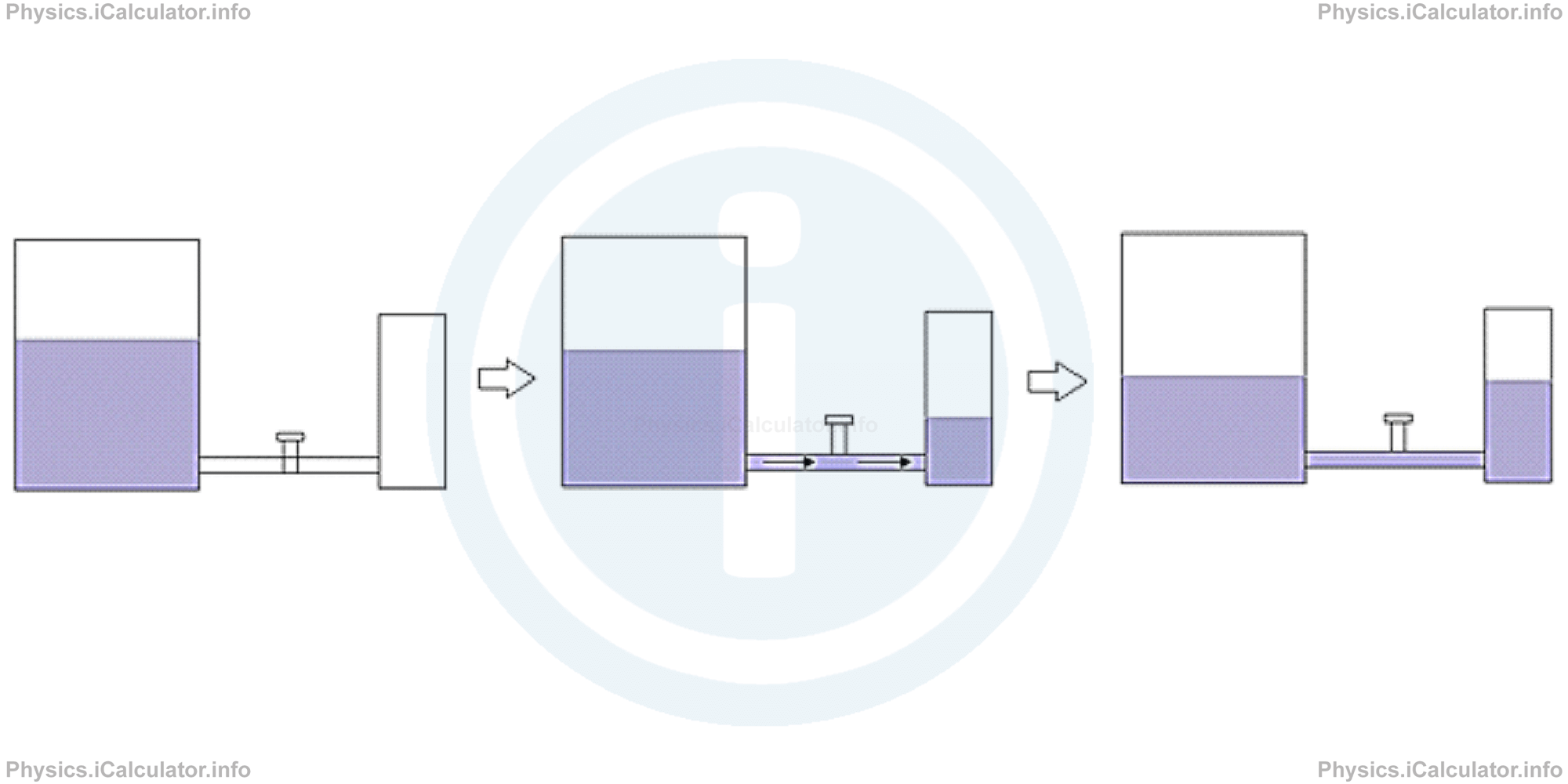
Another example: if containers are not identical, the water flow stops when water reaches the same level in both container, regardless the amount of water they hold.
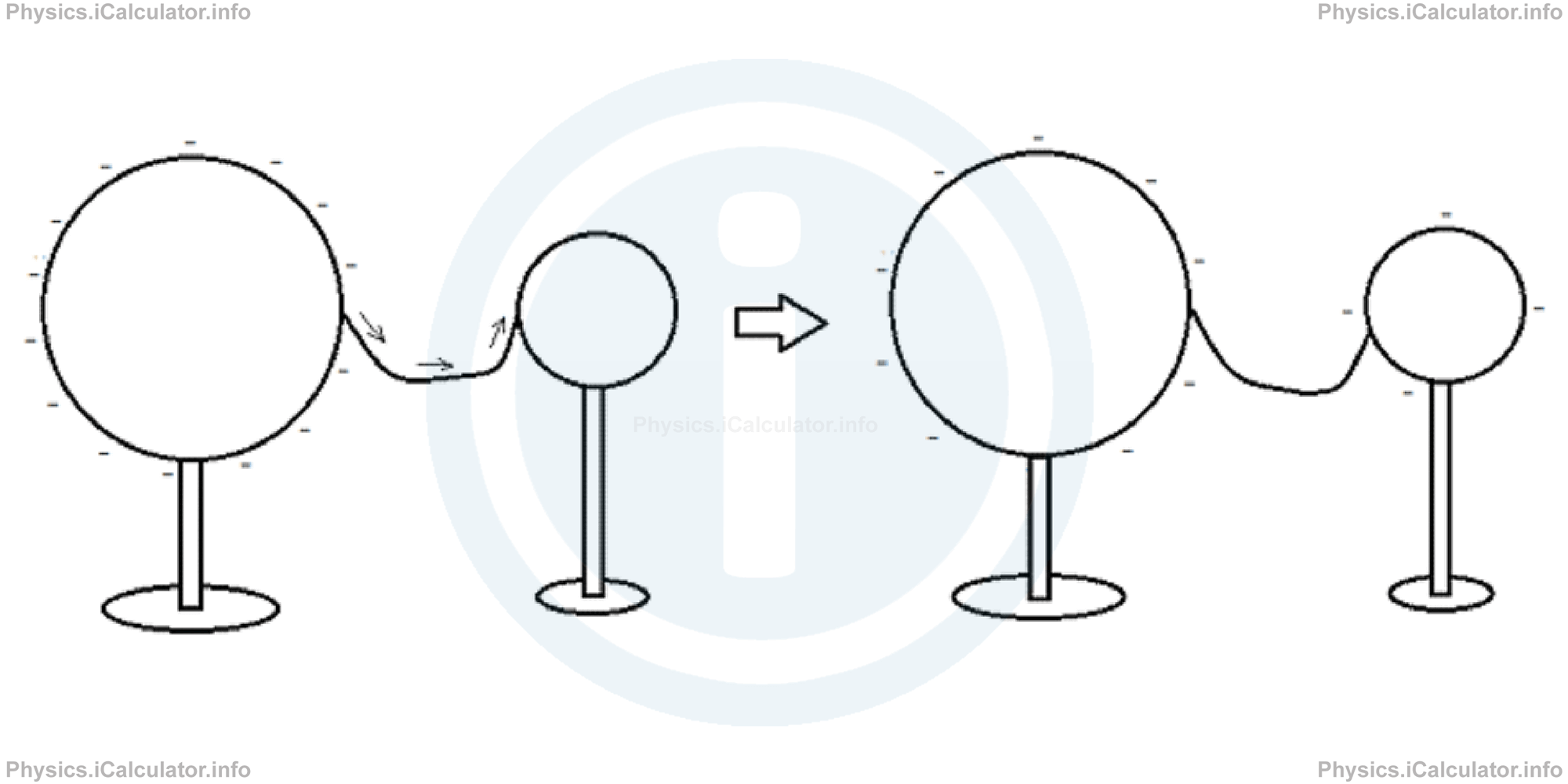
The same phenomenon occurs to electric charges as well. It is not the number of free charges in both ends of a conductor the main factor that determines the electricity flow but it is the current density instead. For example, when we connect together two conducting spheres of different sizes through a conducting wire, the charge flow stops when both spheres reach the same charge density, not the same number of extra charges, as it is obvious the larger sphere will have more extra charges than the smaller sphere when the equilibrium is established.
In the above paragraph there were two concepts mentioned: charge density and current density. They do not represent the same thing. Let's explain their meaning providing some examples as an illustration.
a. Charge Density
Charge density shows how close electric charges are to each other in a conductor. There are three variants of charge density.
- Linear charge density, λ. It shows how close the charges are to each other in a long and very thin conducting wire of length L. Linear charge density is calculated by the equationλ = Q/Land it is measured by Coulombs per metre [C/m].
- Surface charge density, σ. It shows how close the charges are to each other in a surface of area A. Surface charge density is calculated by the equationσ = Q/Aand it is measured by Coulombs per square metre [C/m2].
- Volume charge density, ρ. It shows how close the charges are to each other in a space of volume V. Volume charge density is calculated by the equationρ = Q/Vand it is measured by Coulombs per cubic metre [C/m3].
Example 1
What is the linear charge density along the height, surface charge density and volume charge density if 24 μC of charge are distributed uniformly on the cylinder shown in the figure?
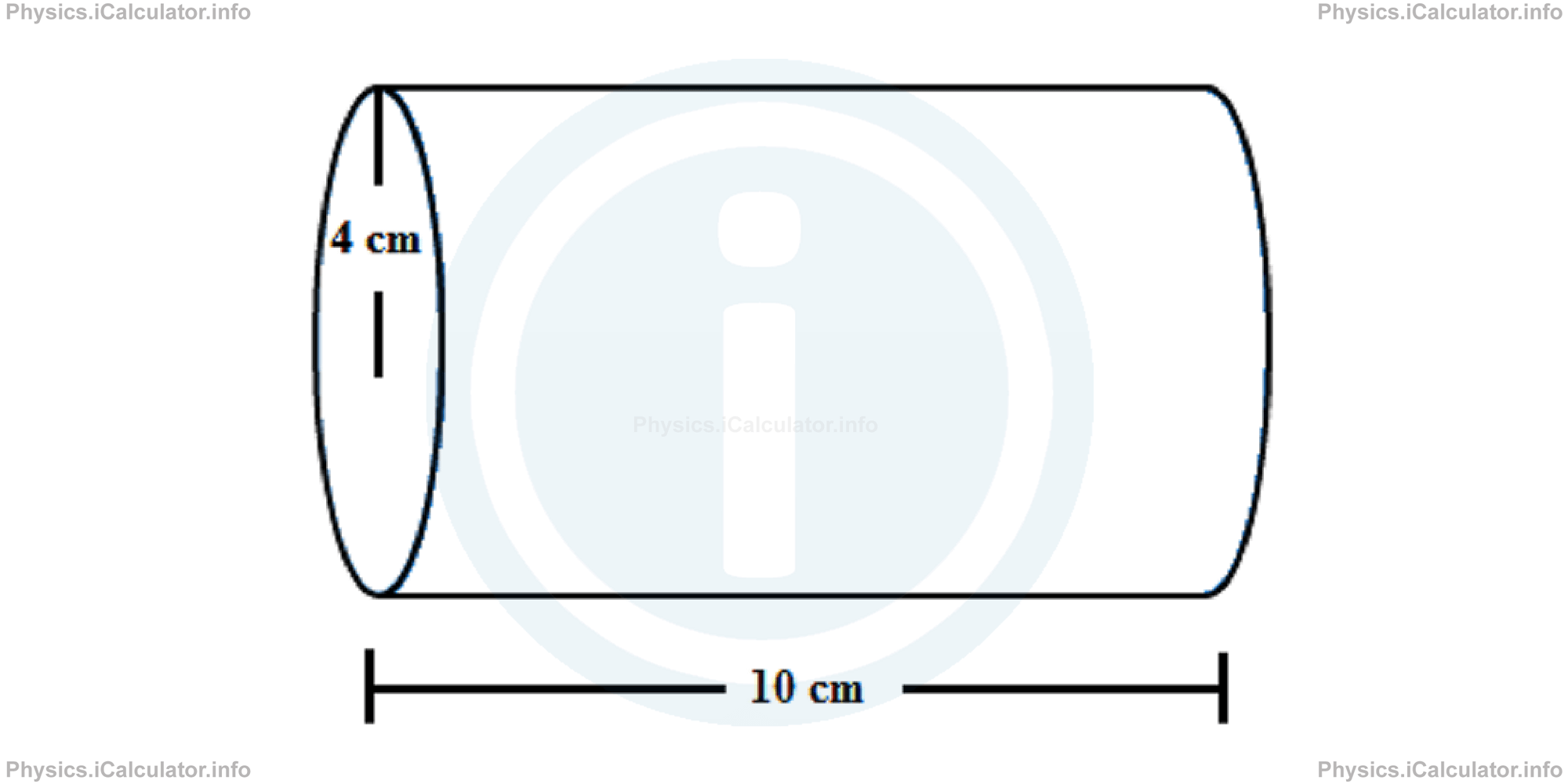
Solution 1
From the figure, we can see that:
L = 10 cm = 0.1 m = 10-1 m
R = 4 cm = 0.04 m = 4 × 10-2 m
Also, we have Q = 24 μC = 2.4 × 10-5 C.
Thus, for the linear charge density, we obtain
= 2.4 × 10-5 C/10-1 m
= 2.4 × 10-4 C/m
Since the total area of cylinder is the sum of the two circular bases and the lateral face (which is a rectangle whose length is equal to base circumference and width is equal to the height of cylinder), we obtain for the surface charge density
= Q/2πR2 + 2πR ∙ h
= Q/2πR ∙ (R + h)
= 2.4 × 10-5 C/2 ∙ 3.14 ∙ 0.04 m ∙ (0.04 m + 0.1 m)
= 2.4 × 10-5 C/3.5 × 10-2 m2
= 0.686 × 10-3 C/m2
= 6.86 × 10-4 C/m2
As for the volume charge density, we have to consider the volume of cylinder, which is
= 3.14 ∙ (4 × 10-2 m)2 ∙ 10-1 m
= 5.024 × 10-4 m3
Therefore, we obtain for the volume charge density
= 2.4 × 10-5 C/5.024 × 10-4 m3
= 4.78 × 10-2 C/m3
Remark! From the results found above, it is more realistic to discuss area charge density than for the other two types of charge density, as it is a known fact that electric charges are distributed throughout the outer surface of a conductor. Only when the amount of charge is too large, free electrons are found inside the inner volume of conductor as well. On the other hand, if the conducting wire is as thin as to allow only one electron flowing through it, then we can discuss about linear charge density.
b. Current Density
Charge density is a quantity that regards situations when there is a kind of equilibrium, i.e. when the charges do not move after being distributed throughout the conductor. It is a known fact that in universe everything is dynamic (in motion) though. Of course, the static approach is very useful to explain the related concepts in an easier way; however, it is the dynamic approach the one that gives us a clearer picture on how the world of electricity works.
For this reason, we introduce the concept of current density, J, which is an extension of that of charge density. Current density is a vector quantity that gives the rate of current flow through a certain area A. Mathematically, the current density is calculated by
where I is the current and A is the area in which the current flows (usually the cross-sectional area of conductor), similar to the area discussed in the tutorial that describes the electric flux explained in the previous chapter.
However, in vector form we use another equation to describe the current density. It is
where ρ is the volume charge density and v is known as the "drift velocity", i.e. the net velocity of charges movement in a certain direction (usually in the direction determined by the push of the electric source along the conducting wire). This is because the charges movement is quite complex due to the continuous collision with other particles; however, we are interested only in the direction in which they can do work, i.e. in the direction in which electricity moves. Drift motion is similar in concept to thermal motion. There is one fundamental difference between these two concepts however. Drift motion gives a resultant in a single direction for all charges (the direction of electrons flow along the conducting wire), while the resultant direction of thermal motion is zero because such a motion is random. (Another difference is that thermal motion regards atoms and molecules of substance while drift motion regards to electric charges only).
Let's prove the equivalence between the two above formulae for current density through the method of dimensional analysis (by considering the units). Thus, when considering the first (scalar) formula, we obtain
= [A]/[m2 ]
= [A/m2 ]
while when considering the second (vector) formula, we obtain
= [C/m3 ] ∙ [m/s]
= [C/(s ∙ m2 )]
= [C/s] ∙ [1/m2 ]
= [A] ∙ [1/m2 ]
= [A/m2 ]
As you see, the units in both cases are equal, so both formulae are true for the current density.
Example 2
Find the drift velocity of an electron moving in a 10 m long copper wire connected to a 12 V battery at room temperature if the mean free time between two collisions is τ = 3 × 10-14 s? Take the charge of electron as e = 1.6 × 10-19 C and its mass is me = 9.1 × 10-31 kg.
Solution 2
The electron accelerates uniformly from rest until it reaches the maximum velocity. This means the average drift velocity is half of the maximum drift velocity, similar to when an object starts moving from rest at constant acceleration in kinematics. Then it stops after hitting another particle, starts accelerating again and so on. This process repeats itself periodically at time intervals τ. Therefore, we can write
= 1/2 ∙ a ∙ τ
= 1/2 ∙ Fe/me ∙ τ
= 1/2 ∙ e ∙ E/me ∙ τ
= 1/2 ∙ e ∙ ∆V/me ∙ d ∙ τ
= e ∙ ∆V ∙ τ/2me ∙ d
= (1.6 × 10^(-19) C) ∙ (12 V) ∙ (3 × 10^(-14) s)/2 ∙ (9.1 × 10^(-31) kg) ∙ (10 m)
= 3.16 × 10-3 m/s
= 3.16 mm/s
This value is very small compared to the velocity of electric current, which is close to the speed of light, i.e. at the order of 105 km/s. This means the effect of electric current is mostly due to its wave effect than due to the charges movement.
You have reached the end of Physics lesson 15.1.2 Charge Density and Current Density. Why are they Different?. There are 4 lessons in this physics tutorial covering Electric Current. Current Density, you can access all the lessons from this tutorial below.
More Electric Current. Current Density Lessons and Learning Resources
Whats next?
Enjoy the "Charge Density and Current Density. Why are they Different?" physics lesson? People who liked the "Electric Current. Current Density lesson found the following resources useful:
- Difference Feedback. Helps other - Leave a rating for this difference (see below)
- Electrodynamics Physics tutorial: Electric Current. Current Density. Read the Electric Current. Current Density physics tutorial and build your physics knowledge of Electrodynamics
- Electrodynamics Revision Notes: Electric Current. Current Density. Print the notes so you can revise the key points covered in the physics tutorial for Electric Current. Current Density
- Electrodynamics Practice Questions: Electric Current. Current Density. Test and improve your knowledge of Electric Current. Current Density with example questins and answers
- Check your calculations for Electrodynamics questions with our excellent Electrodynamics calculators which contain full equations and calculations clearly displayed line by line. See the Electrodynamics Calculators by iCalculator™ below.
- Continuing learning electrodynamics - read our next physics tutorial: Electric Resistance. Combinations of Resistors
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Electric Current. Current Density" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.
Electrodynamics Calculators by iCalculator™
- Amount Of Substance Obtained Through Electrolysis Calculator
- Charge Density Calculator
- Electric Charge Stored In A Rc Circuit Calculator
- Electric Field In Terms Of Gauss Law Calculator
- Electric Power And Efficiency Calculator
- Electron Drift Velocity Calculator
- Equivalent Resistance Calculator
- Force Produced By An Electric Source Calculator
- Joules Law Calculator
- Ohms Law Calculator
- Potential Difference In Rc Circuit Calculator
- Resistance Due To Temperature Calculator
- Resistance Of A Conducting Wire Calculator