Menu
Physics Lesson 7.1.2 - Kinematics of Uniform Circular Motion
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Kinematics of Uniform Circular Motion, this is the second lesson of our suite of physics lessons covering the topic of Kinematics of Rotational Motion, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Kinematics of Uniform Circular Motion
The simplest case of rotational motion is the uniform circular motion which represents objects moving at the same speed (not velocoty) around a fixed point by maintaining a constant distance from it. The reason why velocity is not constant although its magnitude doesn't change, is because the object's moving direction changes continously when it follows a circular path. Remember from Section 2 "Vectors and Scalars" that two vectors are equal only if they have both the same magnitude and direction, not just only the same magnitude or the same direction. Look at the figure below.
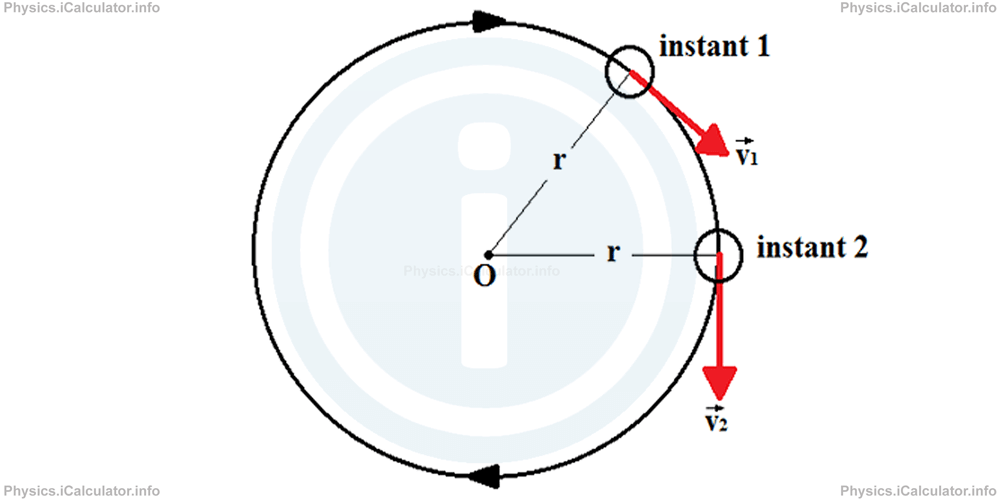
In this figure, velocites of the moving object in the two given instants are different despite having the same magnitude (velocity vectors have the same length). Such velocities of objects moving according peripheral points of a circle (i.e. according the circle's circumference) are known as "tangential velocity, v⃗ " as velocity vector lies according the circle's tangent at every instant.
a. Angle of Rotation (Angular Displacement)
Since in circular motion we are more interested in how an object rotates rather than how it moves, the angle of rotation, φ,, is a very important parameter of such a motion. This angle is measured in radians (rad) and it is also known as "angular displacement". Thus, when an object makes a complete rotation, the angle φ is equal to 2π rad = 2 × 3.14 rad = 6.28 rad (we simply write 2π rad). When an object makes N rotations around a fixed point, the angle of rotation is
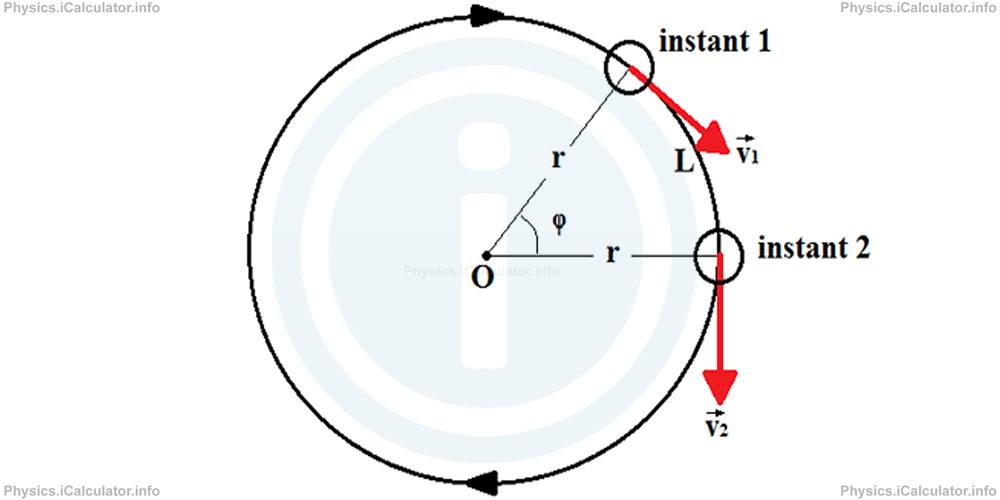
As the angle of rotation represents the surface "wiped" by the radius during rotation, it is analogue to distance in linear motion. Here, we will denote the distance by L instead of the symbol s as used during the study of 1-D Kinemmatics. From geometry, it is known that the magnitude of central angle φ is equal to that of the corresponding arc L. Thus, since a complete arc represent the circumference of circle, where C = 2πr, we have:
φ/2π = L/2πr
φ = L/r
So,
The arc length L represents the distance traveled by the object during its movement when the total angle is φ rad (the value of φ is not limited only in one rotation, i.e. it is not perodical; it depends on the number of rotation an object makes).
Look at the figure:
For example, if an object is moving around a circular path of radius r = 4 m and it makes 20 rotations (N = 20), the total distance travelled by the object is
= r × (N × 2π)
= 4 × 20 × 2 × 3.14
= 502.4 m
b. Angular Velocity
If we divide the angle of rotation by the time this process takes, we obtain another important quantity of rotational motion. It is known as the angular velocity, ω, is measured in radians per second, [rad/s]. Since radian is not a proper dimemsion in itself, we often write 1/s or s-1 for the unit of angular velocity. However, we will write rad/s here to not confuse this unit with that of frequency.
We have
This equation is very similar to the equation of uniform linear motion v = L / t where L is the distance traveled by an object during the time interval t, and v is the obect's speed.
In uniform circular motion, an object moves at the same (both linear and angular) speed. Therefore, we can limit the study of such a motion to a single rotation only. In this case, we use the period T instead of time t, Circumference C = 2πr instead of distance L and the angle of one rotation 2π instead of the total angle φ. Look at the table below:
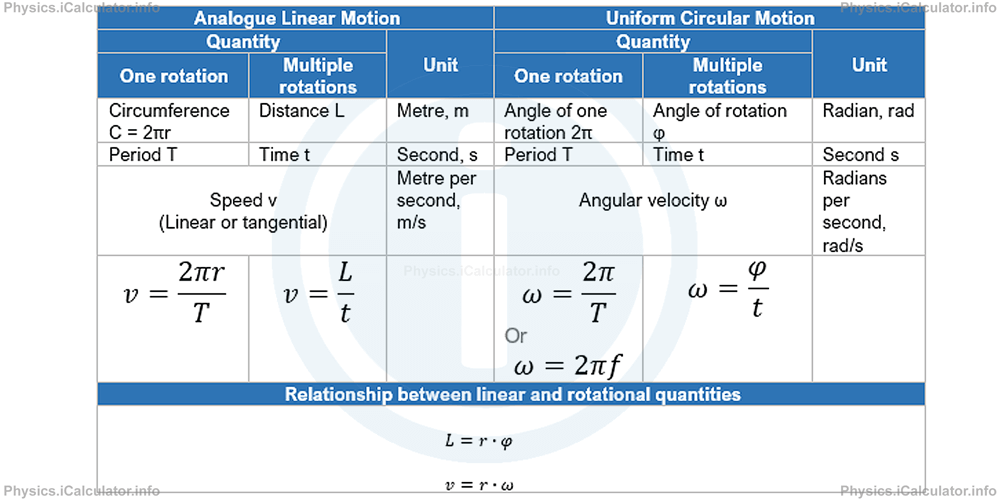
The last equation is obtained by dividing both sides of the previous equation by the time t. Thus,
L/t = r × φ/t
L/t = r × φ/t
v = r × ω
Example 2
A girl has tied a stone at the edge of a 2 m long rope and she rotates it uniformly for 20 s. The stone makes in total 8 revolutions during this interval.
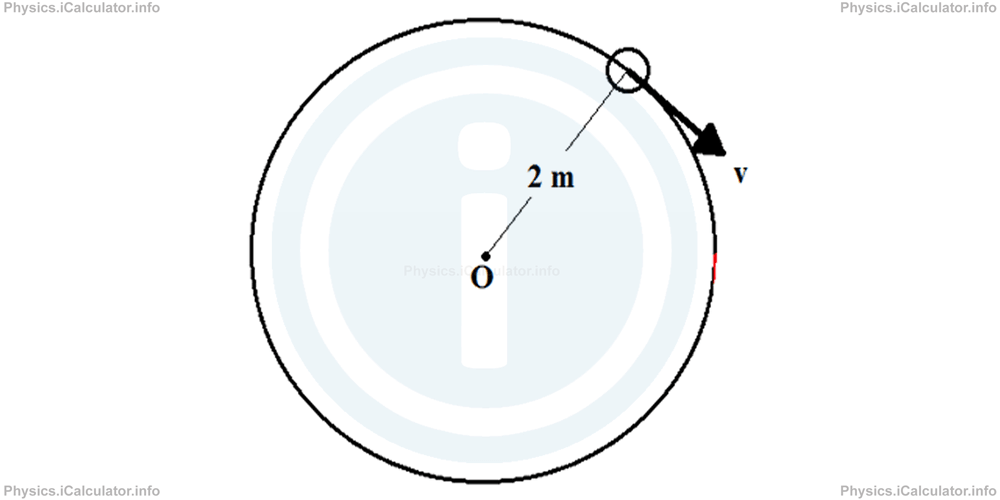
Calculate:
- Period of rotation
- Frequency of rotation
- Angular displacement
- The total distance travelled by the stone
- Tangential speed of the stone
- Angular velocity of the stone
Solution 2
a. Period is the time needed for the object to make one complete revolution. Thus, since the total time is t = 20 s and the number of revolutions is N = 8, we obtain for the period T,
= 20 s/8
= 2.5 s
b. Frequency represents the number or revolution in one second. It is the inverse of period. Thus,
= 1/2.5 s
= 0.4 Hz
c. Angular displacement represents the total angle wiped by the rope during the entire motion. Thus, giving that the angle for one complete rotation is 2π rad (where π ≈ 3.14), for 8 rotations we obtain
= 8 × 2π rad
= 16π rad
d. The total distance travelled by the stone is calculated by using the relationship between the linear and the corresponding circular quantities, i.e. by multiplying the circular quantities by radius to obtain the corresponding circular ones. Thus,
= 2 × 16π
= 2 × 16 × 3.14 m
= 100.48 m
e. Tangential speed of stone can be calculated in many ways. One of them is by dividing the total distance by the total time. Thus,
= 100.48 m/20 s
= 5.024 m/s
f. Angular velocity of the stone is calculated in many ways as well. We can divide the angular displacement by time, divide the tangential speed by radius, multiplying frequency by 2π and so on. Let's use the first method for example. We have:
= 16π rad/20 s
= 0.8 π rad/s
You have reached the end of Physics lesson 7.1.2 Kinematics of Uniform Circular Motion. There are 4 lessons in this physics tutorial covering Kinematics of Rotational Motion, you can access all the lessons from this tutorial below.
More Kinematics of Rotational Motion Lessons and Learning Resources
Whats next?
Enjoy the "Kinematics of Uniform Circular Motion" physics lesson? People who liked the "Kinematics of Rotational Motion lesson found the following resources useful:
- Circular Feedback. Helps other - Leave a rating for this circular (see below)
- Rotation Physics tutorial: Kinematics of Rotational Motion. Read the Kinematics of Rotational Motion physics tutorial and build your physics knowledge of Rotation
- Rotation Revision Notes: Kinematics of Rotational Motion. Print the notes so you can revise the key points covered in the physics tutorial for Kinematics of Rotational Motion
- Rotation Practice Questions: Kinematics of Rotational Motion. Test and improve your knowledge of Kinematics of Rotational Motion with example questins and answers
- Check your calculations for Rotation questions with our excellent Rotation calculators which contain full equations and calculations clearly displayed line by line. See the Rotation Calculators by iCalculator™ below.
- Continuing learning rotation - read our next physics tutorial: Dynamics of Rotational Motion
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Kinematics of Rotational Motion" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.