Menu
Physics Lesson 7.1.3 - Uniformly Accelerated (Decelerated) Rotational Motion
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Uniformly Accelerated (Decelerated) Rotational Motion, this is the third lesson of our suite of physics lessons covering the topic of Kinematics of Rotational Motion, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Uniformly Accelerated (Decelerated) Rotational Motion
Again, we can use the analogy between the linear and circular motion to explain the uniformly accelerated (decelerated) motion, which in itself is part of non-uniform circular motion which we will not discuss here as it is very complicated for the level required in this webpage.
As examples of uniformly accelerated rotational motion we can mention objects that start rotating from rest. Their rotation accelerates until they reach a steady rate. Only then, the rotational motion can be considered as uniform. On the other hand, when a rotation is slowing down until it stops (wheels when a car is slowing down, drum of a washing machine when you turn the power off, etc), we have a uniformly decelerated rotational motion.
a. Initial and final angular velocity
Just as in linear motion, we have an initial and final angular velocity, whose values are not equal. We can write ω0 for the initial and ω for the final angular velocity of a rotating object.
b. Angular acceleration
It is obvious that the change in angular velocity mentioned above, takes a certain time to occur. Hence, we can speak here for a kind of acceleration, known as angular acceleration and is denoted by the symbol alpha (α). From the analogy with linear motion it is very easy to write its formula.
The unit of angular acceleration obviously is [rad/s2] as angular velocity is measured in [rad/s] and the time in [s].
The abovementioned analogy can be extended for the other three equations of uniformly accelerated (deceleration) motion of both types. The following table includes all these formuleae.
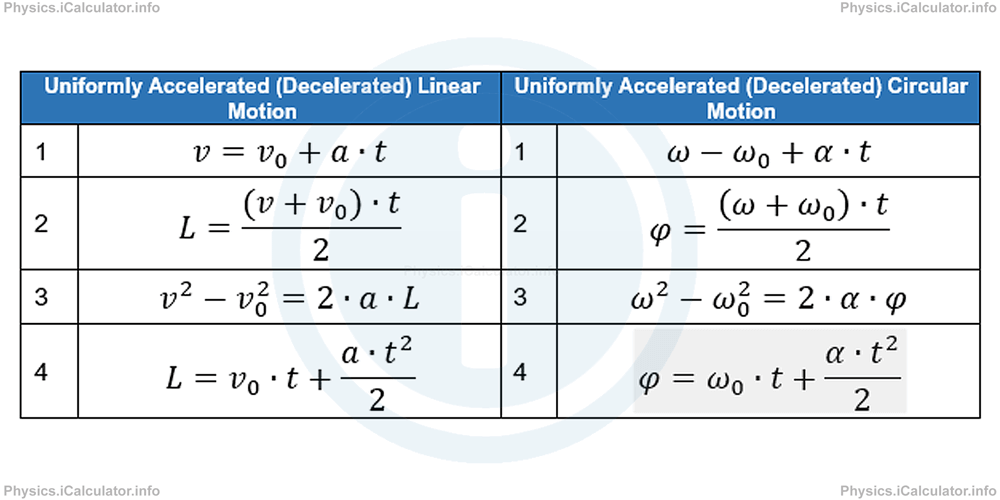
(L is used here to represent the linear distance instead of s, in order to fit the topic discussed here).
Example 3
A platform starts rotating from rest and after 12 s it reaches an angular velocity of 24 rad/s. The platform radius is 4 m and a small object is attached at the edge of platform as shown in the figure.
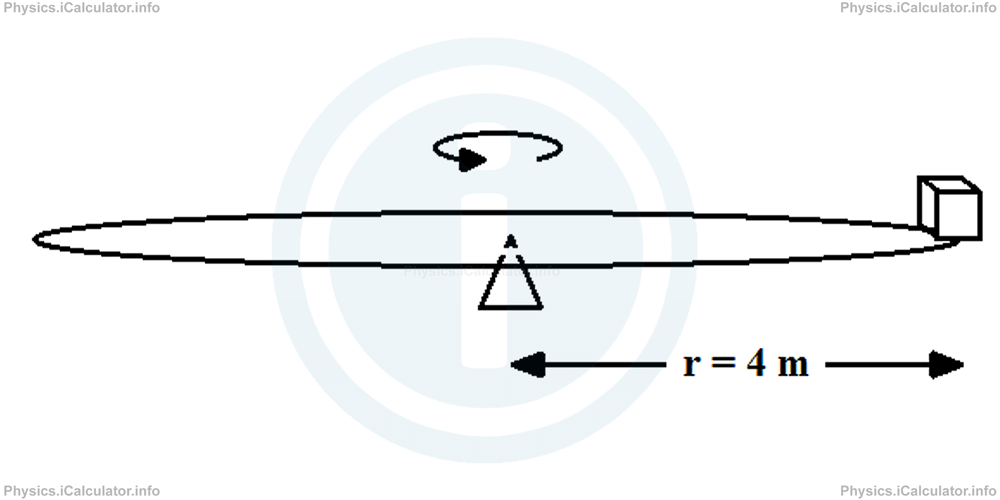
Calculate:
- Angular displacement of the object
- Angular acceleration of the platform
- Total distance travelled by the object
Solution 3
a. From the equation
and giving that ω0 = 0, ω = 24 rad/s and t = 12 s, we obtain for the angular displacement
= 24 × 12/2
= 144 rad
b. Angular acceleration is calculated by the first equation or rotational accelerated motion written in terms of α, as
Substituting the values, we obtain
= 2 rad/s2
c. Distance L is calculated by the equation
where r = 4 m is the radius of the platform. Therefore, we obtain
= 576 m
You have reached the end of Physics lesson 7.1.3 Uniformly Accelerated (Decelerated) Rotational Motion. There are 4 lessons in this physics tutorial covering Kinematics of Rotational Motion, you can access all the lessons from this tutorial below.
More Kinematics of Rotational Motion Lessons and Learning Resources
Whats next?
Enjoy the "Uniformly Accelerated (Decelerated) Rotational Motion" physics lesson? People who liked the "Kinematics of Rotational Motion lesson found the following resources useful:
- Accelerate Feedback. Helps other - Leave a rating for this accelerate (see below)
- Rotation Physics tutorial: Kinematics of Rotational Motion. Read the Kinematics of Rotational Motion physics tutorial and build your physics knowledge of Rotation
- Rotation Revision Notes: Kinematics of Rotational Motion. Print the notes so you can revise the key points covered in the physics tutorial for Kinematics of Rotational Motion
- Rotation Practice Questions: Kinematics of Rotational Motion. Test and improve your knowledge of Kinematics of Rotational Motion with example questins and answers
- Check your calculations for Rotation questions with our excellent Rotation calculators which contain full equations and calculations clearly displayed line by line. See the Rotation Calculators by iCalculator™ below.
- Continuing learning rotation - read our next physics tutorial: Dynamics of Rotational Motion
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Kinematics of Rotational Motion" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.