Menu
Physics Lesson 5.3.2 - Gravitational Potential Energy
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Gravitational Potential Energy, this is the second lesson of our suite of physics lessons covering the topic of Gravitational Potential Energy, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Gravitational Potential Energy
One of the closest synonyms of the term "potential" is "possibility." This means potential energy is the energy that is actually stored in an object but which possibly can be used to do work.
Let's take a simple example from daily life to explain this point. Suppose you have saved ₤30,000 in your bank account. You can use this money to purchase the things you like, maybe put it towards a mortgage or travel around the world. In any case, the initial capital that represents your spending abilities was ₤30,000. When you spend all these money, you are left with zero capital regardless how you spent them.
Likewise, potential energy represents the energy used to bring an object from one point to another, regardless the path. The forces involved in such processes (i.e. processes in which the path followed to do a certain work is not important) are known as "conservative forces."
In the specific case, gravitational potential energy is made possible by the existence of gravitational field (and therefore by the gravitational force) generated by the objects involved in the system. Obviously, one of these objects is the Earth and the other may be any object near its surface. Since all forces generated by a field (distant forces) are all conservative, i.e. their work does not depend on the path followed, we can conclude that gravitational force is a conservative force. Look at the figure below:
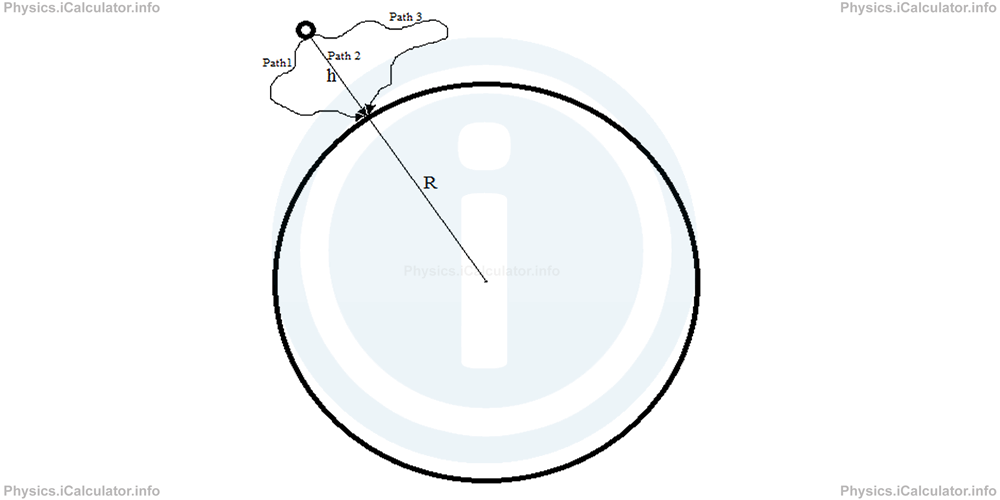
In this figure, there are three possible paths the object may follow when moving from the actual position to the Earth surface. In each case, the object moves from the position R + h to the position R relative to the centre of the Earth, that represents the point in which the Earth's gravitational field is produced.
In the Physics Tutorial "Types of Forces I. Gravitational Force and Weight" we stated that gravitational force is the attraction force between any two objects. We also explained that the equation of gravitational force for an object on Earth surface is
where M is the mass of the Earth, m is the mass of the object, R is the radius of the Earth and G is the gravitational constant. The gravitational potential energy when the object in the figure is on the ground (based on the equation 1), therefore is
= -G × M × m/R2 × R
= -G × M × m/R
On the other hand, when the object was at the position R + h, its gravitational potential energy was
= -G × M × m/(R + h)2 × (R + h)
= -G × M × m/R + h
The change in gravitational potential energy of the object therefore is
Equation 2
∆GPE = GPE2 - GPE1= -G × M × m/R - -G × M × m/(R + h)
= -G × M × m × 1/R - 1/R + h
= -G × M × m × R + h - R/R × (R + h)
= -G × M × m × h/R × (R + h)
We know that gravitational field strength g⃗ is calculated by the formula
For small heights from the ground, i.e. when h << R, we can take R + h ≈ R. Therefore, for the denominator of the fraction in the equation (2) we can write
Hence, substituting the value of g⃗ in the equation of the change in gravitational potential energy and considering the above approximation, we obtain
Equation 3
∆GPE ≈ - G × M × m × h/R2= - m × g × h
This equation represents the simplified formula of gravitational potential energy. It is widely used for objects near the Earth surface. It is very suitable because we don't need to take in consideration the mass and the radius of the Earth but only the mass of the object and its height from the ground.
When we calculate the gravitational potential energy using the simplified equation
we presume that the final GPE (i.e. GPE2) is zero. Therefore, we have
Equation 4
∆GPE = GPE2 - GPE1=0 - GPE1
= - GPE1
Combining equations (3) and (4), we obtain for the gravitational potential energy of an object at a height h above the ground:
or
Equation 5
GPE1 = m × g × hThe above equations (including the signs) are interpreted as follows:
When we send an object from the ground (GPE1 = 0) to a certain height (GPE2 = m × g × h), we increase its gravitational potential energy, i.e. we work against the gravity. Therefore, we do the work:
= - ( -m × g × h)
= m × g × h
For example, when we raise a 2 kg object at 3 m above the ground, we do
of work against the gravity. The sign minus before g means the object decelerates when moving upwards. As a result, work is negative But when we lower a 20 kg object from h = 5 m on the ground (h = 0), we do
in the direction of gravity. Therefore, work here it positive.
To summarize all explained above, we can write:
Since W = - ΔGPE, the change in GPE when an object moves from the ground to a certain height or vice versa is
The sign in the above equation depends on the direction of process. When the object moves up, its GPE increases, so the sign of ΔGPE is positive (and therefore, work is negative). This means we are doing work against gravity. When the object moves down, its GPE decreases, so the sign of ΔGPE is negative (and therefore, work is positive). This means we are doing work in the direction of gravity.
Example 1
Three 70 kg men come down from the same height in three different directions as shown in the figure.
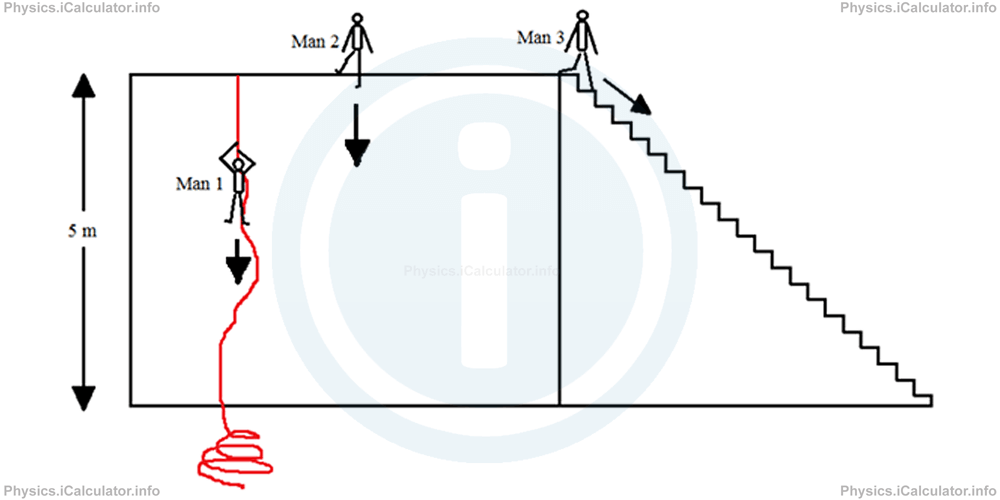
The first man uses a rope to come down, the second man jumps from the initial position while the third man goes down the stairs.
- What is the change in gravitational potential energy for each of them?
- What can you say about the routes followed?
Solution 1
a. Since initially all the three men are at the same height (h1 = 5 m) the initial gravitational potential energy for each of them is
= 70kg × 9.81 N/kg × 5m
= 3433.5J
By the end of process, they will have again the same height from the ground (now h2 = 0). Therefore, their final gravitational potential energy is
= 70kg × 9.81 N/kg × 0m
= 0J
Therefore, the change in gravitational potential energy for each man is
= 0 - GPE1
= 0 - 3433.5 J
= -3433.5 J
The above result means the gravitational potential energy of all the three men decreases by 3433.5 J.
b. Since the change in gravitational potential energy is the same for all the three men regardless the route followed, we can say that gravitational potential energy does not depend on the path but only on the initial and final positions of the object(s) involved. This is because gravitational force (which is caused by the gravitational field) is a conservative force.
You have reached the end of Physics lesson 5.3.2 Gravitational Potential Energy. There are 3 lessons in this physics tutorial covering Gravitational Potential Energy, you can access all the lessons from this tutorial below.
More Gravitational Potential Energy Lessons and Learning Resources
Whats next?
Enjoy the "Gravitational Potential Energy" physics lesson? People who liked the "Gravitational Potential Energy lesson found the following resources useful:
- What Feedback. Helps other - Leave a rating for this what (see below)
- Work, Energy and Power Physics tutorial: Gravitational Potential Energy. Read the Gravitational Potential Energy physics tutorial and build your physics knowledge of Work, Energy and Power
- Work, Energy and Power Revision Notes: Gravitational Potential Energy. Print the notes so you can revise the key points covered in the physics tutorial for Gravitational Potential Energy
- Work, Energy and Power Practice Questions: Gravitational Potential Energy. Test and improve your knowledge of Gravitational Potential Energy with example questins and answers
- Check your calculations for Work, Energy and Power questions with our excellent Work, Energy and Power calculators which contain full equations and calculations clearly displayed line by line. See the Work, Energy and Power Calculators by iCalculator™ below.
- Continuing learning work, energy and power - read our next physics tutorial: Elastic Potential Energy and Combination of Springs
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Gravitational Potential Energy" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.