You are here:
  1. / iCalculator
  2. / Thermodynamics
  3. / Kinetic Theory Of Gases
  4. / Variables

Menu

Physics Lesson 13.6.6 - State Variables and Path-Dependent Variables

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 1 Votes ]

Welcome to our Physics lesson on State Variables and Path-Dependent Variables, this is the sixth lesson of our suite of physics lessons covering the topic of The Kinetic Theory of Gases. Ideal Gases, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.

State Variables and Path-Dependent Variables

a) State variables

For a fixed amount of gas, we can find the temperature if we know the pressure and volume of the gas. Consider the example below:

Example 6

A P - V diagram for 0.2 moles of an ideal gas is shown below. Determine the initial and final temperatures of the gas sample.

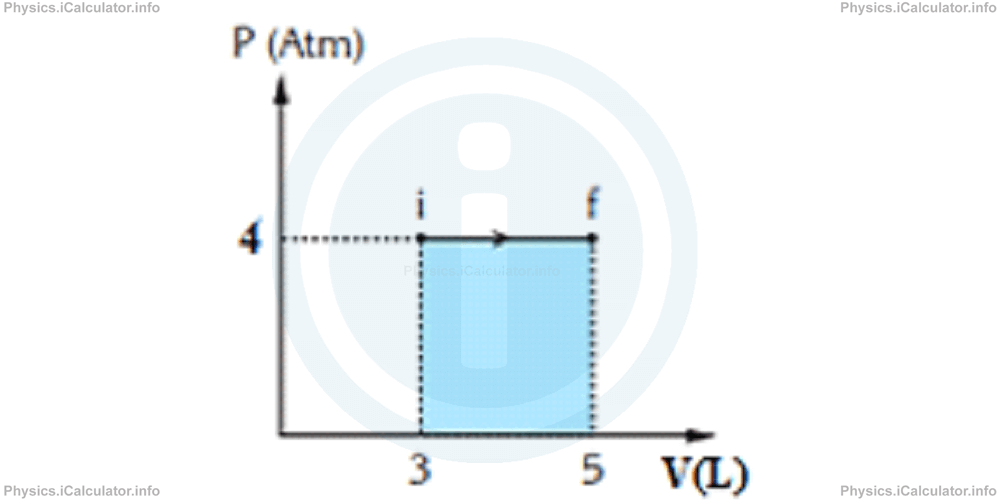
Physics Tutorials: This image provides visual information for the physics tutorial The Kinetic Theory of Gases. Ideal Gases

Solution 6

In the graph, "i" stands for initial and "f" for final state of the gas. Let's apply the ideal gas law for the points i and f given that P1 = P2 = P = 4 atm = 400 000 Pa, Vi = 3 L = 0.003 m3 and Vf = 5 L = 0.005 m3. We have for the initial state i:

P × Vi = n × R × Ti

Thus,

Ti = P × Vi/n × R
= 100 000 × 0.003/0.2 × 8.31
= 180.5 K

For the final state, we have:

P × Vf = n × R × Tf
Tf = P × Vf/n × R
= 100 000 × 0.005/0.2 × 8.31
= 300.8 K

We draw two conclusions from the above example:

  1. Every point on a P - V diagram has a definite temperature for a fixed amount of gas.
  2. The points on a P - V diagram are called "states". A gas can undergo an infinite number of intermediate states when it moves from the initial to the final state (from i to f).

As explained earlier, pressure, volume and temperature are known as "state variables". This means all these three quantities have an infinite number of values from the initial to the final state. These values either change slowly or remain constant during a thermodynamic process.

Internal energy is also a state variable. Internal energy of a gas sample is a function of temperature only. For a definite amount of gas, every specific temperature value corresponds to a specific amount of internal energy. Therefore, for a given state, the internal energy of gas has a fixed value. When the gas sample returns to the previous state, the internal energy takes the previous value as well.

State variables are macroscopic parameters. For a given state, a gas sample has fixed values of P, V, T and U. Although the speed or energy of a certain molecule are in continuous change, the values of state variables are determined by an average of effects produced by billions of molecules.

b) Path-dependent variables

Heat and work are not state variables. It is meaningless if we talk about heat or work contained in a system. Internal energy is a property of a system. Heat and work are not properties of system in a given state, but characteristics of the process between two states. Remember, both heat and work represent energies transferred between systems.

Consider two different processes between two fixed states as shown in the graph below:

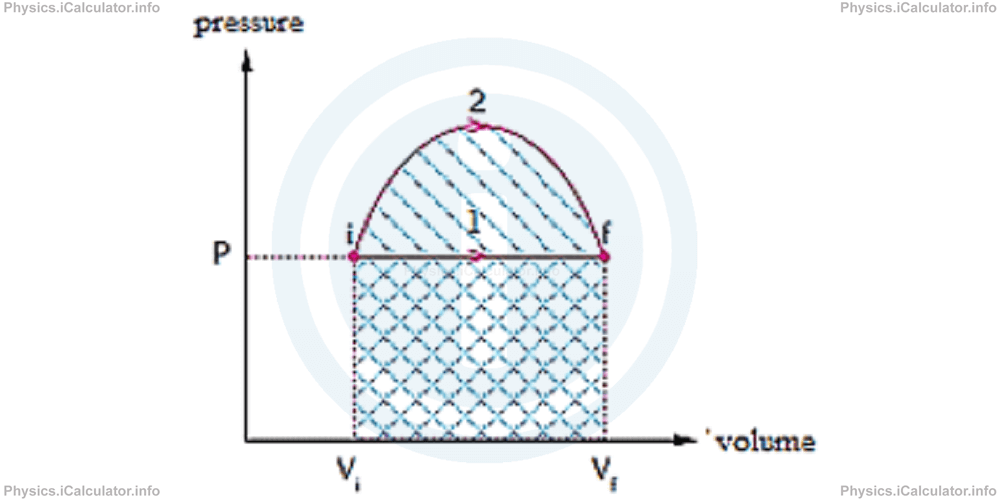
Physics Tutorials: This image provides visual information for the physics tutorial The Kinetic Theory of Gases. Ideal Gases

In the process 1 (path 1) the gas expands at constant volume.

When the gas undergoes the process 2 (path 2), it expands from the same initial state to the same final state as in the process 1, but during the process 2 pressure is first increased then decreased to the original value, probably by placing and removing weights on the piston.

Let's compare the change in the internal energy ΔU, work W and heat Q during the two above processes.

Since the temperatures Ti and Tf have fixed values in the states "i" and "f" regardless of the intermediate stages, we have T1 = T2. Since for a gas sample equal changes in temperatures imply equal changes in internal energy, we can write:

∆U1 = ∆U2

Comparing the areas under the P - V graphs (which correspond to the works in each process), we conclude that

W1 < W2

Applying the First Law of Thermodynamics Q = ΔU + W for both states 1 and 2, we obtain

Q1 < Q2

Hence, we conclude that although the initial and final states are the same, the gas sample absorbs more heat when it moves along the path 2, because it does more work along this path. This is like walking from one village to another along two different paths: one requires climbing over a hill, the other walking along a horizontal path. Both paths bring us to the same destination, but one of them requires much more energy compared to the other.

It is clear from the above example that heat and work depend not only on the initial and final states, but also on the intermediate states the gas undergoes during a thermodynamic process. Therefore, heat and work are not state variables, because they depend on the path followed between the initial and final states. Such variables are called "path-dependent variables".

You have reached the end of Physics lesson 13.6.6 State Variables and Path-Dependent Variables. There are 6 lessons in this physics tutorial covering The Kinetic Theory of Gases. Ideal Gases, you can access all the lessons from this tutorial below.

More The Kinetic Theory of Gases. Ideal Gases Lessons and Learning Resources

Thermodynamics Learning Material
Tutorial IDPhysics Tutorial TitleTutorialVideo
Tutorial		Revision
Notes		Revision
Questions
13.6The Kinetic Theory of Gases. Ideal Gases
Lesson IDPhysics Lesson TitleLessonVideo
Lesson
13.6.1The Meaning of Mole. Avogadro's Number
13.6.2Ideal Gases
13.6.3The Ideal Gas Law
13.6.4Work in a Thermodynamic Process
13.6.5Finding Work using a P - V Diagram
13.6.6State Variables and Path-Dependent Variables

Whats next?

Enjoy the "State Variables and Path-Dependent Variables" physics lesson? People who liked the "The Kinetic Theory of Gases. Ideal Gases lesson found the following resources useful:

  1. Variables Feedback. Helps other - Leave a rating for this variables (see below)
  2. Thermodynamics Physics tutorial: The Kinetic Theory of Gases. Ideal Gases. Read the The Kinetic Theory of Gases. Ideal Gases physics tutorial and build your physics knowledge of Thermodynamics
  3. Thermodynamics Revision Notes: The Kinetic Theory of Gases. Ideal Gases. Print the notes so you can revise the key points covered in the physics tutorial for The Kinetic Theory of Gases. Ideal Gases
  4. Thermodynamics Practice Questions: The Kinetic Theory of Gases. Ideal Gases. Test and improve your knowledge of The Kinetic Theory of Gases. Ideal Gases with example questins and answers
  5. Check your calculations for Thermodynamics questions with our excellent Thermodynamics calculators which contain full equations and calculations clearly displayed line by line. See the Thermodynamics Calculators by iCalculator™ below.
  6. Continuing learning thermodynamics - read our next physics tutorial: Pressure, Temperature and RMS Speed

Help others Learning Physics just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 1 Votes ]

We hope you found this Physics lesson "The Kinetic Theory of Gases. Ideal Gases" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.

Thermodynamics Calculators by iCalculator™

© iCalculator™ 2009 - 2024 | Physics Calculators | Privacy Policy | Terms of Use | Contact