Physics Lesson 18.1.2 - Galilean Transformations

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Physics lesson on Galilean Transformations, this is the second lesson of our suite of physics lessons covering the topic of Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.

Galilean Transformations

Let's consider an inertial reference frame S which we assume at rest and another inertial reference frame S' moving at constant velocity v in respect to S. An object is moving horizontally at velocity v in the system S in the moving direction of S'. It is obvious that this object will be at rest in respect to the inertial system S' as they are moving at the same velocity and direction (v' = 0).

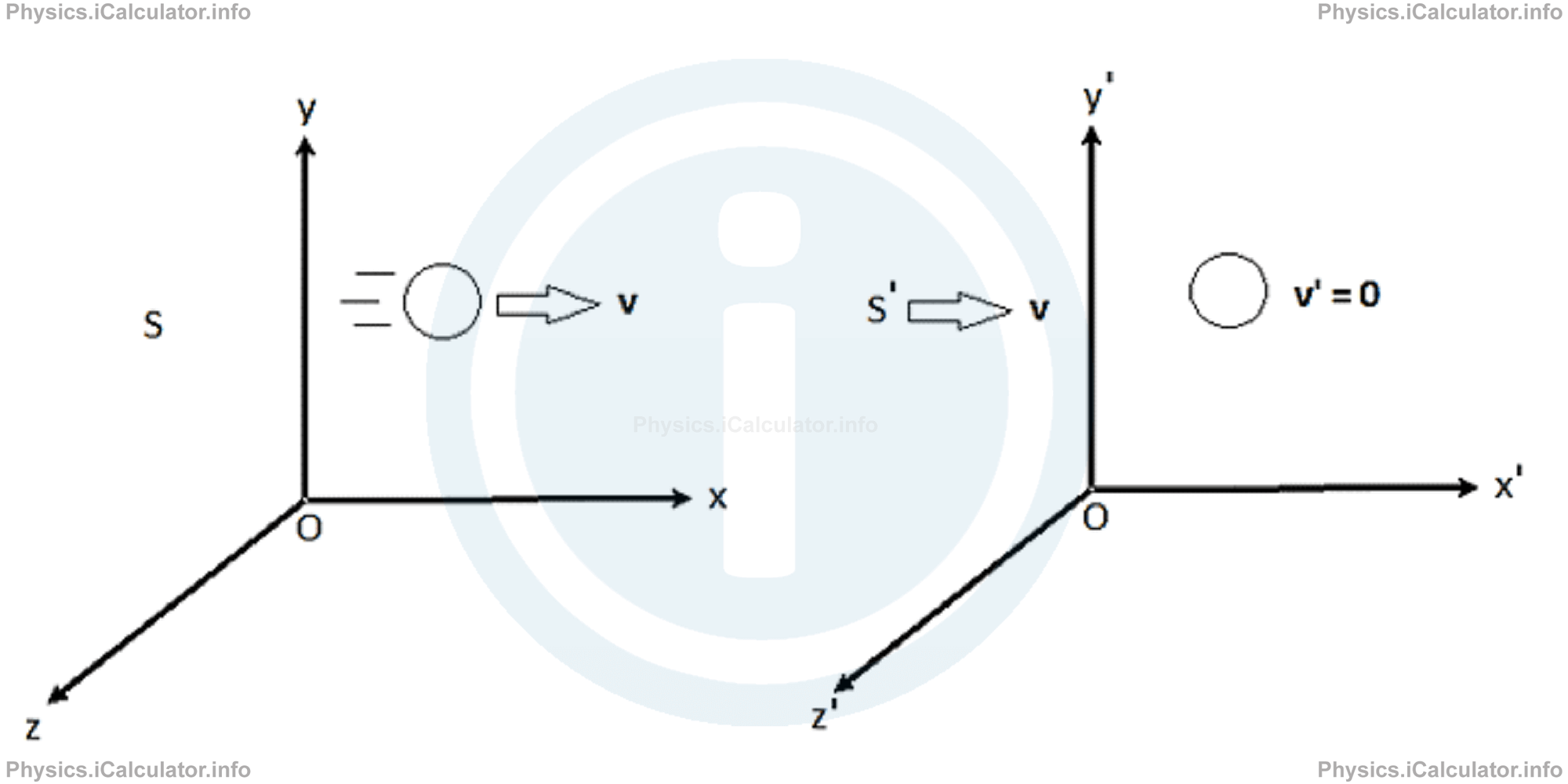
We want to know how to determine the coordinates in S' when we know them in frame S. In the figure above, in the S frame the object is moving and the {x, y, z} axes are fixed. When we transform to the S' coordinate system (so that {x', y', z'} are at rest), it now looks like the object has velocity v' = 0 and that the old axes {x, y, z} are moving with velocity - v in the NEGATIVE x' direction. In this case, "v" appears as the relative velocity of the PRIMED coordinate system {x', y', z'} or S', compared to the UNPRIMED coordinate system {x, y, z} or S.

To determine the object's coordinates in the inertial frame, S', when we know its coordinates in the original inertial frame, S, we employ the Galilean space and time transformations. If S' has a velocity relative to S so that v' = 0, then we have:

In Galilean transformations, time is the same in all inertial frames.

If the objects moves in three dimensions, its velocity v contains three non-zero components v_x, v_y and v_z. Therefore, the Galilean transformations if the inertial frame of reference S' moves at the same velocity v, become:

In the example discussed in the previous paragraph, the observer at rest is thought as being at rest in respect to the inertial system S, while the passenger inside the moving car is at rest in respect to the system S' which has its origin at any point inside the car and which is moving at constant velocity v in respect to the system S. This moving velocity of the inertial system S' represents the car's velocity. Let's see an example to clarify this point.

Example 1

Two cars A and B are moving toward each other at constant speeds v_A = 20 m/s and v_B = 10 m/s respectively as shown in the figure.

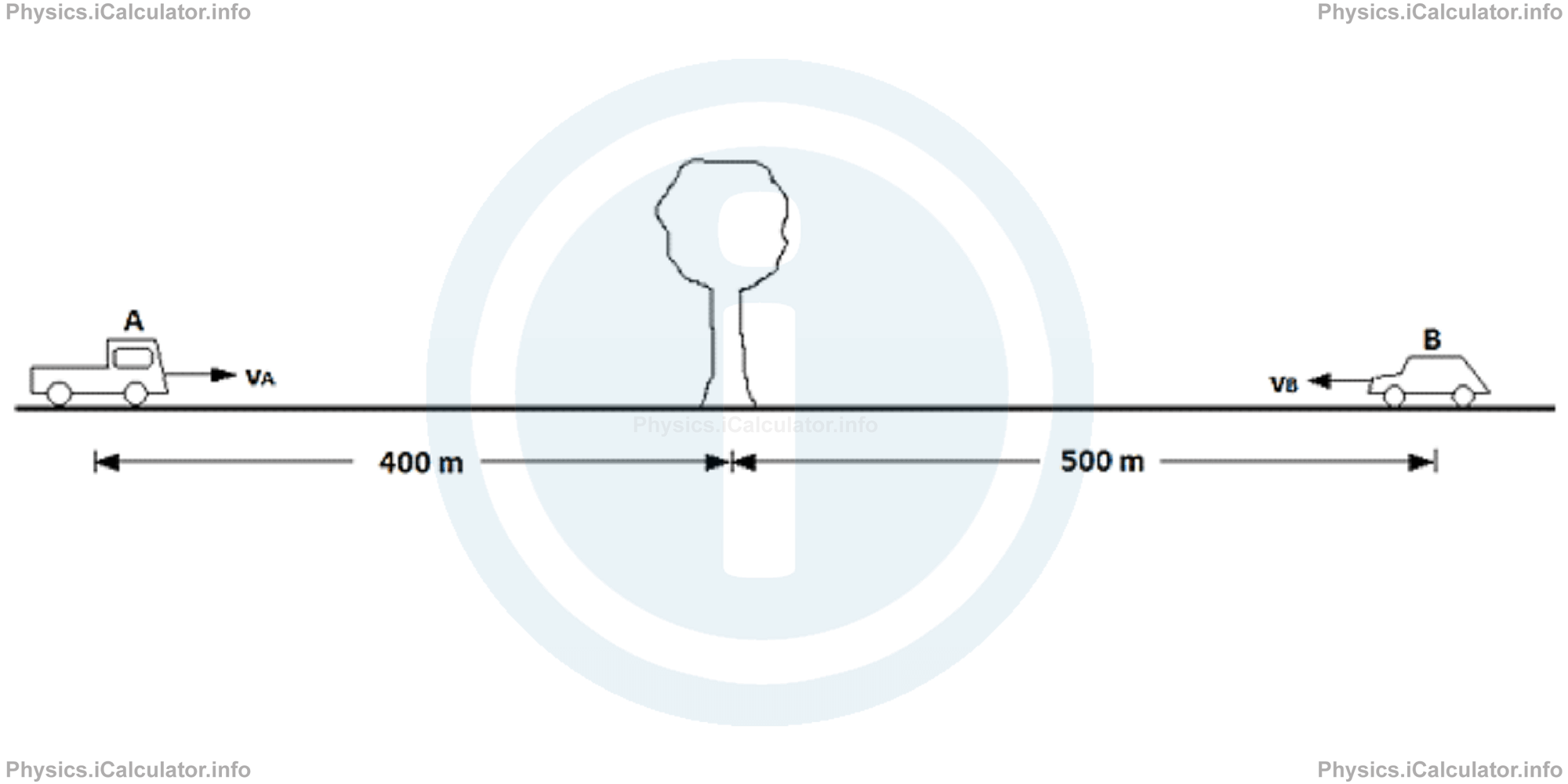
The car A is initially 400 m on the left of the tree, while the car B is initially 500 m on the right of the tree. Find the initial position of the tree is you choose:

1. Position of the tree as origin of the inertial system of reference
2. Position of the car A as origin of the inertial system of reference
3. Position of the car B as origin of the inertial system of reference

In addition, find:

4. Equations of motion for each car in each inertial reference system
5. Position of the meeting point for the two cars in each inertial reference system

Solution 1

1. If we take the position of the tree as origin of the inertial reference system and assume as positive the left-to-right direction in the figure, we obtain for the initial position x_0T of the tree (and also the position of tree at any instant):
   x_0T = x_T = 0 m
2. If we take the position of car A as origin of the inertial reference system and assume the positive direction due right of the figure, we obtain for the initial position of tree:
   x_0T = + 400 m
3. If we take the position of car B as origin of the inertial reference system and assume the positive direction due right of the figure, we obtain for the initial position of tree:
   x_0T = -500 m
4. If we choose the tree position as origin of reference frame, we have for the initial position of car A: x_0A = - 400 m and for the speed of car A: v_A = + 20 m/s. Therefore, since the general equation of motion for the car A at any reference frame is
   x_A (t) = x_0A + v_A ∙ t
   then, the equation of car A when the tree is chosen as origin, is
   x_A (t) = -400 + 20 ∙ t
   Using the same approach, we find for the car B when the tree is chosen as origin: x_0B = + 500 m and v_B = -10 m/s. Therefore, since the general equation of car B for this reference frame is
   x_B (t) = x_0B + v_B ∙ t
   we obtain after substitutions
   x_B (t) = 500-10 ∙ t
   When the car A is chosen as origin of the inertial reference system, then the car A is at rest, and moreover, the initial position x^'_0A is also zero. Thus, since
   x^'_A (t) = x^'_0A + v^'_A ∙ t
   we obtain after substitutions
   x^'_A (t) = 0 + 0 ∙ t
   This means the car A will always be at position 0 for this inertial reference frame.
   As for the car B when the position of car A is chosen as origin, we have x^'_0B = + 400 m + 500 m = + 900 m and the velocity of the car B in respect to the car A is
   v^'_B = v_B-v^'_A = -10 m/s-20 m/s = -30 m/s
   Therefore, since the general equation of car B when the car A is chosen as origin is
   x^'_B (t) = x^'_0B + v^'_B ∙ t
   we obtain after substituting the known values:
   x^'_B (t) = 900-30 ∙ t
   On the other hand, when the car B is chosen as origin of the inertial reference frame, we have for the initial position of car A:
   x^''_0A = -400m-500m = -900 m
   and for the velocity of car A:
   v^''_A = v_B-v^'_A = 0-(-30 m/s) = 30 m/s
   Hence, since the general equation of the car A when the car B is chosen as origin is
   x^''_A (t) = x^''_0A + v^''_A ∙ t
   we obtain after substituting the known values:
   x^''_A (t) = -900 + 30 ∙ t
   As for the car B, it is considered always at rest if the car B itself acts as origin. Thus, we have
   x^''_0B and v^''_B = 0
   Thus, we obtain for the equation of car B in this reference frame:
   x^''_B (t) = x^''_0B + v^''_B ∙ t
   or
   x^''_B (t) = 0 + 0 ∙ t
   Again here, the car B is considered at rest during the entire process if the origin of the inertial reference frame is in this car.
5. The two cars meet if their coordinates are equal. The time is also taken the same as the two events are simultaneous. Thus, if we choose the tree as origin, we must write for the meeting point:
   x_A (t) = x_B (t)
   Thus, substituting the expressions obtained in (d), we obtain
   -400 + 20 ∙ t = 500 - 10 ∙ t
   20 ∙ t + 10 ∙ t = 500 + 400
   30 ∙ t = 900
   t = 30 s
   Thus, using any of equations of motion for this inertial system of reference (for example that of the car A), we obtain for the meeting position in respect to the tree:
   x_A (t) = -400 + 20 ∙ t
   = -400 + 20 ∙ 30
   = -400 m + 600 m
   = + 200m
   This means the two cars meet 200 m on the right of the tree.
   The same result could also have been obtained if we used the equation of the car B. Thus,
   x_B (t) = 500 - 10 ∙ t
   = 500 - 10 ∙ 30
   = 500 m - 300 m
   = 200 m
   Moreover, we obtain the same result for any car taken as origin at any inertial reference frame. Let's check this claim. Thus, since the time is equal for each inertial system of reference, we have in case when we take the car A as origin:
   x^'_A (t) = 0 + 0 ∙ t
   = 0 + 0 ∙ 30
   = 0
   and
   x^'_B (t) = 900-30 ∙ t
   = 900 - 30 ∙ 30
   = 900 m - 900 m
   = 0
   This result is understandable; the position of meeting point must correspond to the origin of reference frame when the car A is chosen as inertial reference system because the meeting point always correspond to the position of car A. The same this can be said when we choose the car B as origin. In this case, we have
   x^''_A (t) = -900 + 30 ∙ t
   = -900 + 30 ∙ 30
   = -900 m + 900m
   = 0
   and
   x^''_B (t) = 0 + 0 ∙ t
   = 0 + 0 ∙ 30
   = 0

Remark! When any of cars is chosen as origin and we are interested to find their meeting point, the tree is not involved in calculations as it is out of interest for the event. This is why the tree position is not mentioned in the last two inertial reference systems.

You have reached the end of Physics lesson 18.1.2 Galilean Transformations. There are 5 lessons in this physics tutorial covering Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws, you can access all the lessons from this tutorial below.

More Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws Lessons and Learning Resources

Whats next?

Enjoy the "Galilean Transformations" physics lesson? People who liked the "Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws lesson found the following resources useful:

1. Galilean Transformations Feedback. Helps other - Leave a rating for this galilean transformations (see below)
2. Relativity Physics tutorial: Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws. Read the Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws physics tutorial and build your physics knowledge of Relativity
3. Relativity Revision Notes: Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws. Print the notes so you can revise the key points covered in the physics tutorial for Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws
4. Relativity Practice Questions: Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws. Test and improve your knowledge of Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws with example questins and answers
5. Check your calculations for Relativity questions with our excellent Relativity calculators which contain full equations and calculations clearly displayed line by line. See the Relativity Calculators by iCalculator™ below.
6. Continuing learning relativity - read our next physics tutorial: Classical Principle of Relativity

Help others Learning Physics just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Physics lesson "Relativity. Galilean Transformations. Einstein's Postulates and Newton's Laws" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.

Relativity Calculators by iCalculator™

• Energy Calculator In Relativistic Events
• Frequency Calculator During Doppler Effect In Relativistic Events
• Length Calculator In Relativistic Events
• Lorentz Transformation Of Coordinates Calculator
• Lorentz Transformation Of Velocity Calculator
• Mass And Impulse Calculator In Relativistic Events
• Time Calculator In Relativistic Events
• Velocity Calculator In Relativistic Events