Menu
Physics Lesson 11.2.1 - Wave Function. General Equation of Waves
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Wave Function. General Equation of Waves, this is the first lesson of our suite of physics lessons covering the topic of General Equation of Waves, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Wave Function. General Equation of Waves
As you may have noticed in the previous tutorial, the waves motion is periodical. This means it has many similarities with both circular motion and SHM. The graph of waves is sinusoidal just like in SHM.
However, as stated above (and as seen in the examples of the previous tutorial), since we are dealing with travelling waves, i.e. with waves that are displaced from the original position, when studying their behavior, we need to consider three quantities instead of two: the x- and y-coordinates versus time t. Therefore, the equation of waves must be of the type
where the horizontal position x and the time t are taken as independent variables (values are inserted by the user) while the vertical position y is to be calculated (it is a dependent variable).
Remember that in none of the other abovementioned topics we had such a situation involving three variables. Two variables (one independent and the other dependent) were enough to describe in full such motions. Thus, in circular motion, the equation has the form r(t) where r is the radius of circle and t is the time, while in SHM, the equation of motion is of the form x(t) or θ(t) depending on the type of SHM (linear or rotational).
Hence, given that the wave equation has a sinusoidal form, we write its general form as
You are familiar with most quantities shown in the above equation. Thus,
ymax represents the amplitude A of a point of the wave, as it oscillates according the y-axis,
ω represents the angular frequency (ω = 2π / T as usual),
x is the horizontal position,
t is the time of motion, and
y(x, t) is the vertical position at a given instant.
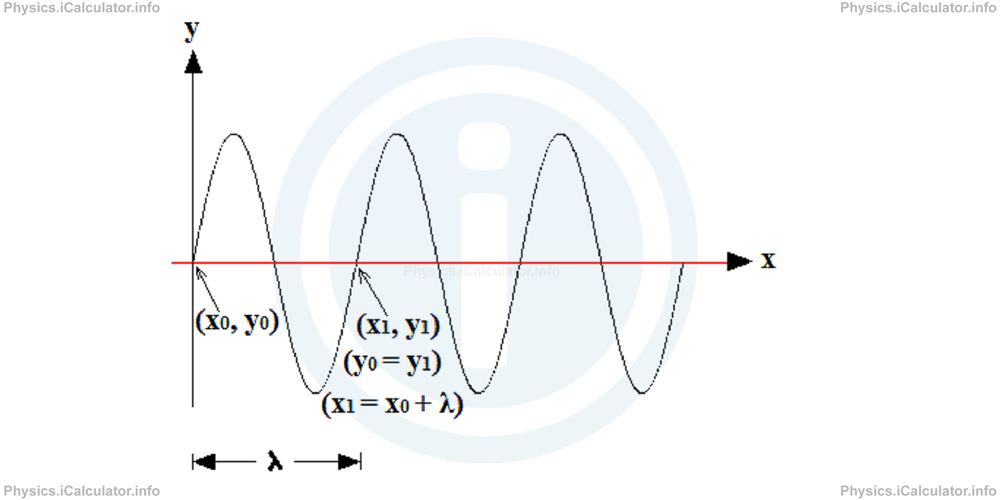
The quantity k is known as the angular wave number. Let's find its relationship with the other known quantities discussed above. Thus, at t = 0, we have
When one cycle is completed, the y-values (the displacement) repeat themselves while the x-values increase by one wavelength λ. Thus, at x = x1 we have
As stated above, we have the same y-coordinate (y0 = y1) for two x-coordinates that change by λ units after a time t1 = T (period). Hence, the equation of wave becomes
= ymax × sin[k × (x0 + λ)]
= sin(k × x0 + k × λ)
Given that
and since the sine functions repeat themselves after every 2π change in x-coordinate, we obtain
Therefore, we obtain for the angular wave number k
In this way, the wave equation becomes
Also, since ω = 2π/T, we can also insert the period T in the wave equation. Therefore, it becomes
In this way, we inserted the values of wavelength and period in the equation of waves, so now it is more complete.
Look at the figure.
It must be noted that the argument
or
represents the phase of the wave equation.
If there is a phase shift φ from the original position of wave, we insert its value in the equation of waves. Thus, it becomes
Remark! The sign minus in the argument (k × x - ω × t) is when the wave moves in the positive direction. When the wave moves towards negative, the argument takes the positive sign, i.e. it becomes (k × x + ω × t).
Example 1
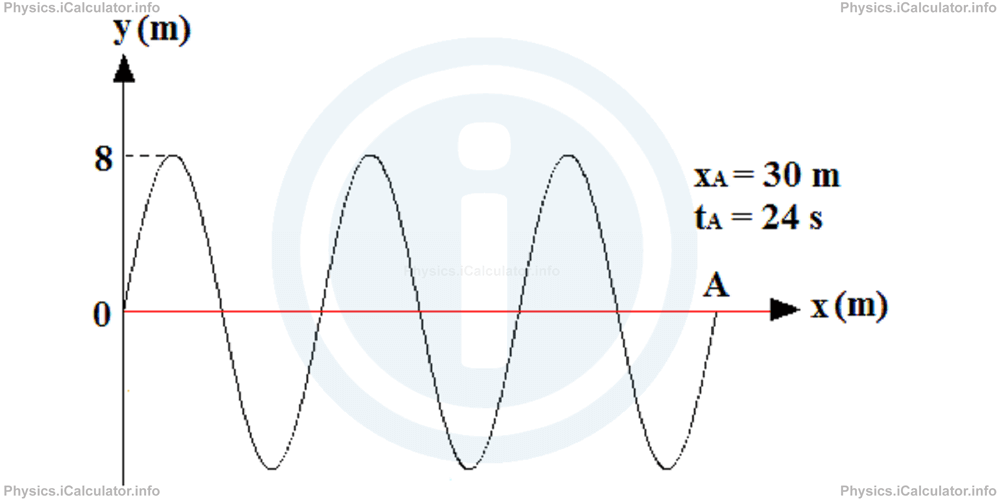
Calculate the y-coordinate of the wave shown in the figure below at t = 2.4 s using the information provided in the graph.
Solution 1
From the graph we see that amplitude ymax = 8 m. Also, the number N of cycles when the wave reaches the point A = 3. Given that the wave in that instant is at xA = 30 m, we obtain for the wavelength
The wave starts from the origin, therefore φ = 0.
Also, given that tA = 24 s, we obtain for the period T:
The horizontal position x at t = 2.4 s can be calculated through the cross-product method. We can denote by B the point at which the wave is at tB = 2.4 s. Thus, given that the wave moves at constant speed, we can write
30 m - 0/24 s - 0 = xB - 0/2.4 s - 0
30/24 = xB/2.4
xB = 30 × 2.4/24
= 3 m
Now, we have everything we need to calculate the vertical position at the given instant. Thus, from the equation
we find after substituting the values,
= 8 × sin(6π/10 - 4.8π/8)
Given that both fractions give the same value, we can find the y-value by ignoring one independent variable, for example t. Thus, we obtain
= 8 × 0.951
= 7.608 m
This means the wave point at t = 2 s (or at x = 3 m) is 7.608 m above the equilibrium position.
You have reached the end of Physics lesson 11.2.1 Wave Function. General Equation of Waves. There are 3 lessons in this physics tutorial covering General Equation of Waves, you can access all the lessons from this tutorial below.
More General Equation of Waves Lessons and Learning Resources
Whats next?
Enjoy the "Wave Function. General Equation of Waves" physics lesson? People who liked the "General Equation of Waves lesson found the following resources useful:
- Function Feedback. Helps other - Leave a rating for this function (see below)
- Waves Physics tutorial: General Equation of Waves. Read the General Equation of Waves physics tutorial and build your physics knowledge of Waves
- Waves Revision Notes: General Equation of Waves. Print the notes so you can revise the key points covered in the physics tutorial for General Equation of Waves
- Waves Practice Questions: General Equation of Waves. Test and improve your knowledge of General Equation of Waves with example questins and answers
- Check your calculations for Waves questions with our excellent Waves calculators which contain full equations and calculations clearly displayed line by line. See the Waves Calculators by iCalculator™ below.
- Continuing learning waves - read our next physics tutorial: Energy and Power of Waves
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "General Equation of Waves" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.