Menu
Physics Lesson 18.3.3 - Dilation of Time and Contraction of Length
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Dilation of Time and Contraction of Length, this is the third lesson of our suite of physics lessons covering the topic of Space and Time in Einstein Theory of Relativity, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Dilation of Time and Contraction of Length
a. Relativistic Dilation of Time
In the previous paragraph, we saw that the simultaneity of events is relative; two events that may be synchronous in one system may not be synchronous in another inertial system (the thought experiment with the bus). In addition, we explained that the time itself is not absolute but relative (t ≠ t').
Now, we will compare time intervals between two events in two different inertial frames (systems) of reference. For this, we use the time measurements taken in a physical event described below.
A wagon is moving at constant velocity due right. We denote the inertial system connected to the wagon by S'. There is a light source A (for example a laser) at bottom-middle of wagon and a receiver R and a standard clock O' very close to the position of the light source.
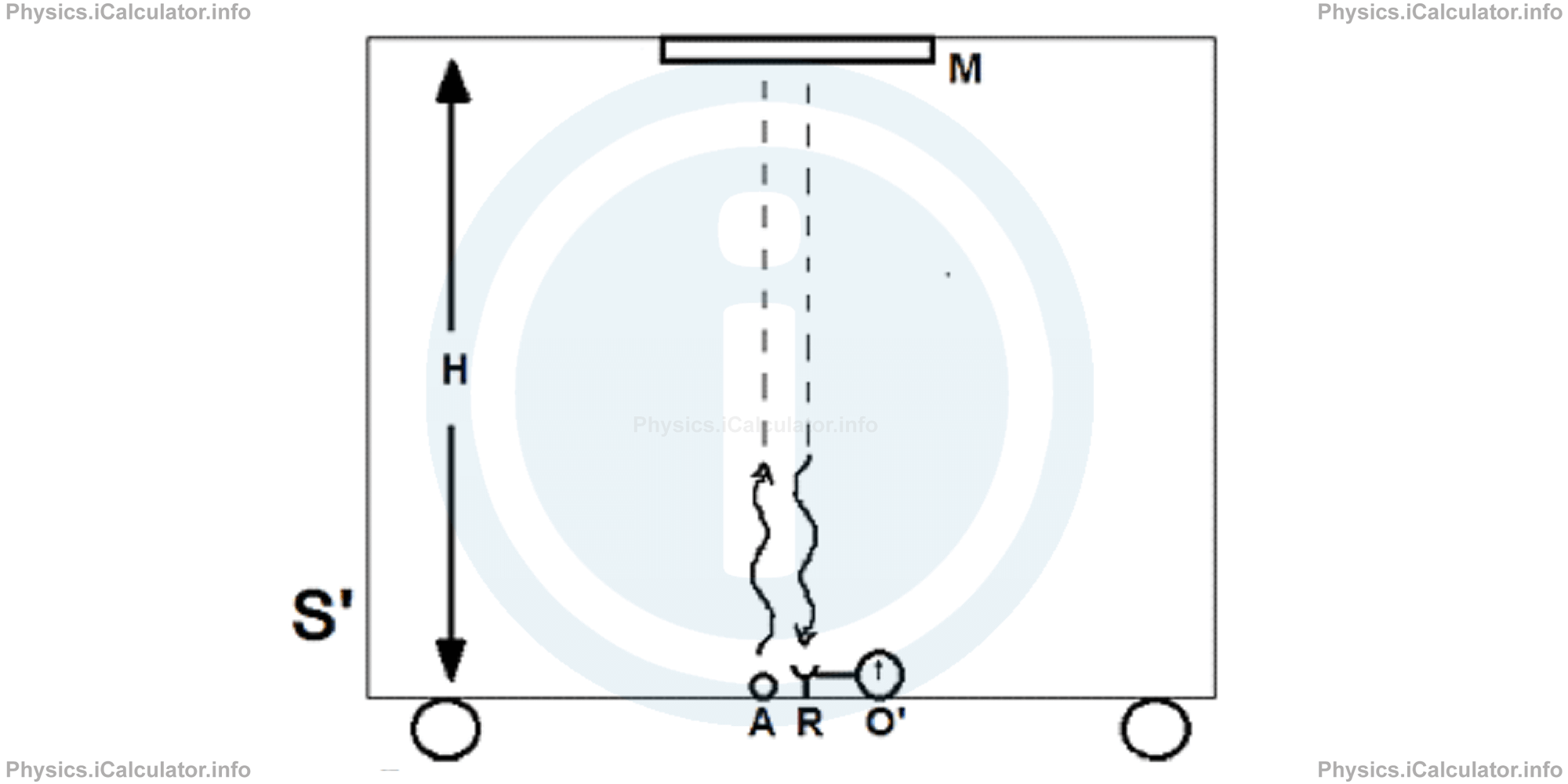
A mirror M is placed at the ceiling of wagon, at the height H from the floor. When a light signal is emitted vertically upward by the source A, it is reflected back by the mirror M and falls to the receiver R. During this process, the time interval Δt' measured by the clock O' is
where c is the speed of light.
Now, let's see what measures an observer outside the wagon, who is at rest with the tracks (the inertial system S). If the train (including the given wagon) moves due right at velocity (V⃗), the light path is not anymore only vertical, as due to the horizontal displacement of the train. Obviously this velocity must be large enough to be considered, i.e. it must be comparable to the speed of light.
In the following figures, there are three instants included: the first figure shows the instant in which the light signal is emitted by the source A, the second figure shows the instant at which the light signal reaches the mirror M and the third figure shows the instant in which the reflected light reaches the receiver R.
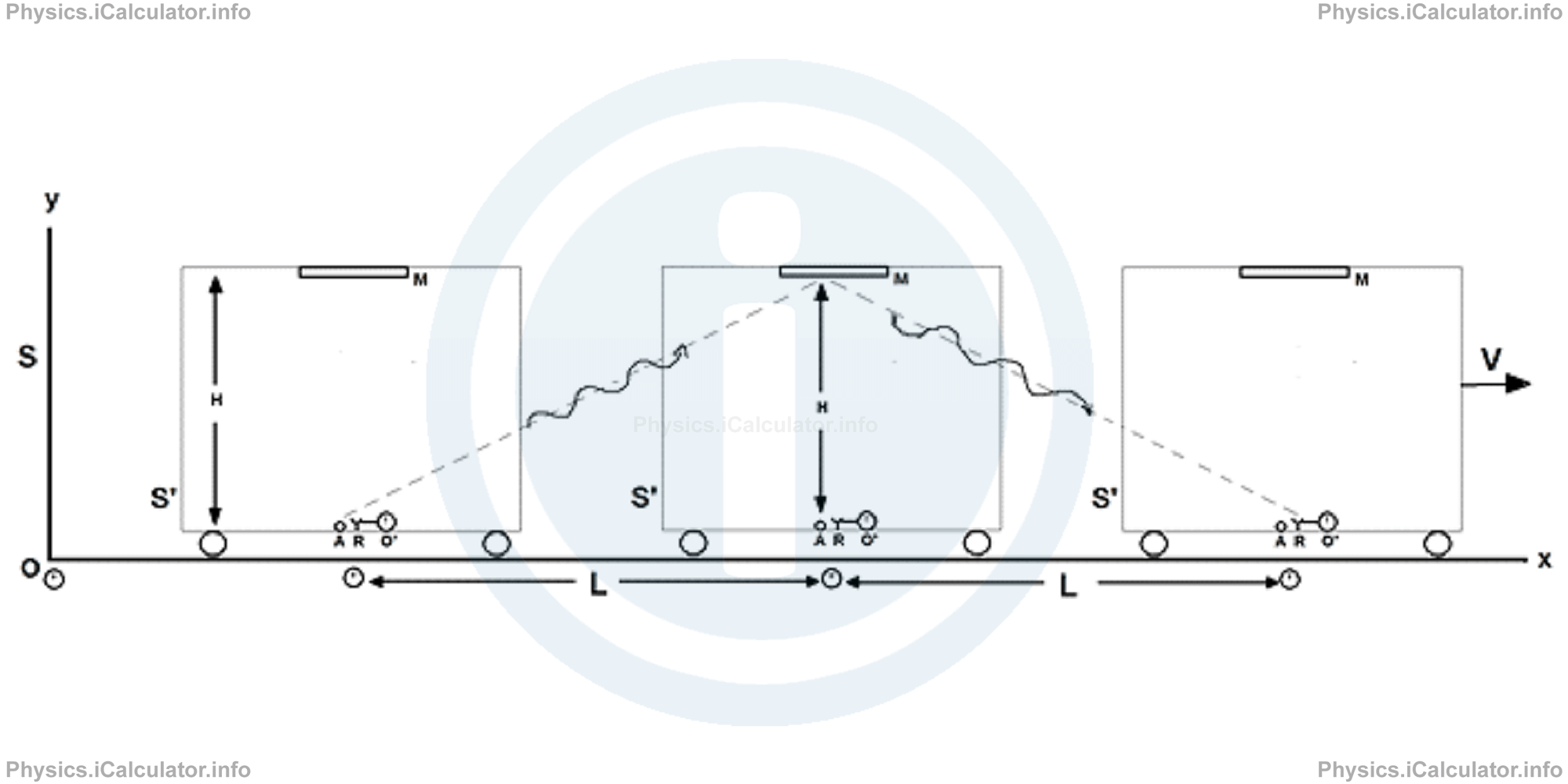
Since the x-coordinate (in the system S) of source, receiver, and mirror (including the clock inside the wagon) change with time in the direction of motion, the two events - the emission of light signal and its receive from the receiver - do not occur at the same point of the space (in the system S). Therefore, the light path is not vertical despite it is still moving at speed c. This new path is longer than the (vertical) path followed by the light ray when viewed from inside the wagon (in the system S'). The time interval (recorder by the three synchronized clocks shown under the wagon) for the light ray to travel the path source A - mirror M - receiver R is Δt.
Since the train is moving at uniform velocity V⃗, we have:
where 2L is the horizontal distance travelled by the train during this event. On the other hand, from Pythagorean Theorem, it is clear that the distance (path) d travelled by the light ray during this process is:
We are considering the same event; so the time interval Δt can also be expressed as
Combining the last three equations, we obtain (giving that H = c · Δt'/2)
= 2 ∙ √(V ∙ ∆t/2)2 + (∆t' ∙ c/2)2 /c
Raising both sides of the above equation in power 2 to remove the square root, we obtain
(∆t)2 = V2 ∙ (∆t)2 + c2 ∙ (∆t')2/c2
(∆t)2 = V2 ∙ (∆t)2/c2 + c2 ∙ (∆t')2/c2
c2 ∙ (∆t)2 = V2 ∙ (∆t)2 + c2 ∙ (∆t')2
c2 ∙ (∆t)2 - V2 ∙ (∆t)2 = c2 ∙ (∆t')2
(∆t')2 = c2 ∙ (∆t)2/c2 - V2 ∙ (∆t)2/c2
(∆t')2 = (∆t)2 - V2 ∙ (∆t)2/c2
(∆t')2 = (∆t)2 ∙ 1 - V2/c2
∆t' = ∆t ∙ √1 - V2/c2
Obviously, the expression within the square root is less than 1 because V < c and V2/c2 is a number between 0 and 1. This means the value of square root itself is a number between 0 and 1 as well. This means Δt' < Δt. In other words, the time measured by the clocks inside the wagon (system S') measure a smaller time (work slower) for the same event when compared to the clocks placed outside the wagon (those of the system S). In other words, any time interval that measures the duration of an event in an inertial system considered at rest, is √1 - V2/c2 times shorter than the corresponding time interval for the same event when it occurs in an inertial system moving at velocity V⃗ relative to the system at rest. Therefore, we say the time dilates (expands) when the event duration is measured in an inertial system moving at velocity V⃗ in respect to the system considered at rest.
Einstein gave a funny explanation when repeatedly asked about the relativity of time. He said: "When you sit with a nice girl for two hours you think it's only a minute, but when you sit on a hot stove for a minute you think it's two hours. That's relativity."
Example 2
A spaceship moving at 0.4 c goes to a star which is 10 light years away from Earth and turns back without staying any second there. Calculate:- The time of this trip measured by a clock placed on Earth surface
- The time measured for the same event by a clock placed inside the spaceship
Solution 2
- The event measured by the clock on the Earth surface lasts for ∆t = 2d/V = 4 l.y. + 4 l.y./0.4 c = 8/0.4 = 20 years
- When the same event is recorded by using the clock inside the spaceship, we obtain for the duration of this event ∆t' = ∆t ∙ √1 - V2/c2As you see, the time flows in different pace in two inertial systems moving at speed relative to each other.
= 20 yrs ∙ √1 - (0.4 c)2/c2
= 20 yrs ∙ √1 - 0.16 c2/c2
= 20 yrs ∙ √1 - 0.16
= 20 yrs ∙ √0.84
= 20 yrs ∙ 0.9165
= 18.33 years
b. Relativistic Contraction of Length
Now we will see that the length of objects or paths measured in two inertial systems of reference is also relative, unlike in the classical theory of relativity. Recall the Galilean transformations, in which the distance between two points (or the length of an object) doesn't change, whatever inertial system you choose to take the measurements - transformations that now look outdated.
Let's consider again a wagon moving at velocity V⃗ along a horizontal path (tracks) as we did in the previous paragraph. At the left end of wagon there is a light source A which emits light rays in the horizontal direction. At the right of wagon there is a mirror M, which reflect the rays back to the source A.
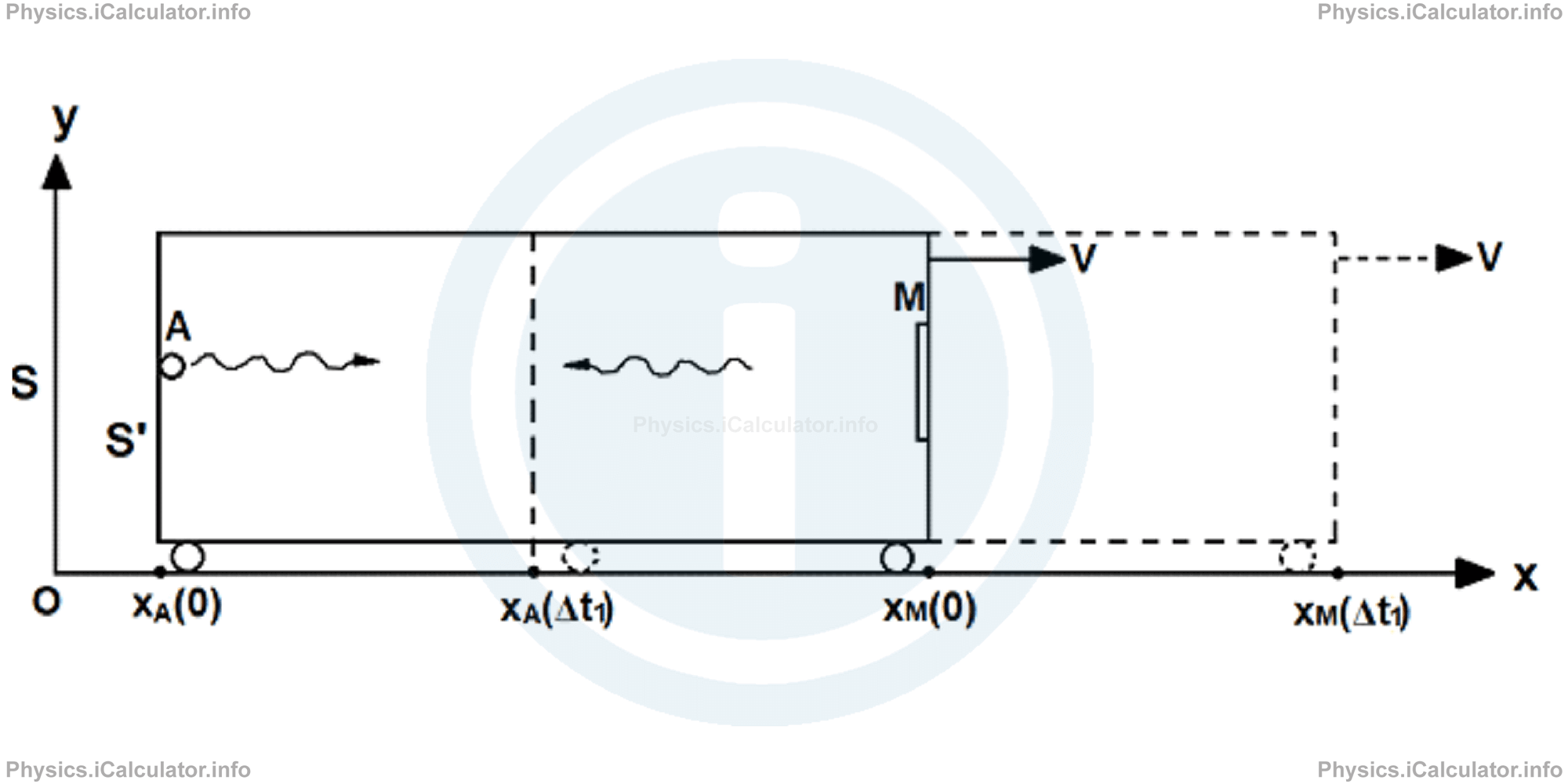
Obviously, the y-direction here is useless as the light source emits signals only in the horizontal direction. Any observer inside the wagon (in the system S') measures a length of L' that corresponds to the distance AM. It is clear that the distance travelled by the light ray viewed from inside the wagon is 2L', where L' is the length of wagon measured from inside it. In addition, all clocks inside the wagon show the time Δt' for the event that regards the emission of a light signal and its return to the receiver (located at A) after being reflected by the mirror M.
Now, let's consider an observer at rest outside the wagon (in the system S). If we synchronize the clocks of the two systems to show the values 0 at the moment of the light ray emission, we have the value xA(0) for the initial position of light source and xM(0) the initial position of mirror. Therefore, the length of wagon viewed from outside the wagon is L = xM (0) - xA(0). When the light signal goes to the mirror M (after a time interval Δt1), the new x-coordinates of source and mirror will be xA(Δt1) and xM(Δt2) respectively.
After the time t' has elapsed, the source is at the new coordinate xA(Δt1) and the mirror is at xM(Δt1). For the observer connected to S, the distance travelled by the light signal during its motion from source to mirror is L + V · Δt1. Therefore, we have
or
Now, let's denote by Δt2 the time (measured from S) needed for the light source to move from mirror to receiver (adjacent to source). Using a similar reasoning as for Δt1, we obtain
Thus, the entire interval Δt needed for the light ray to move from the source to the mirror and back to the source again, is
= L/c - V + L/c + V
= L ∙ (c + V) + L ∙ (c-V)/(c-V) ∙ (c + V)
= 2L ∙ c/c2 - V2
Dividing both numerator and denominator by c2, we obtain
Hence,
Now, let's compare this value with the time interval Δt' obtained for the same event but viewed from inside the wagon (in the system S'). Obviously, this time interval is
In the previous paragraph, we found that
Therefore, we have
2L'/c = √1 - V2/c2 ∙ 2L/c ∙ 1 - V2/c2
2L'/c = 2L/c ∙ √1 - V2/c2
L' = L/√1 - V2/c2
Thus, we obtain
As you see, the length of a moving wagon viewed from outside is shorter than when it is measured from inside. For this reason, the above formula is known as the formula of relativistic contraction of length. This contraction is not because of any force of compression exerted inwards; rather, it is related only to relativistic effects caused due to the motion of wagon at very high speed, comparable to the speed of light.
When we did the same experiment emitting the light vertically, there was no change in height H of the wagon. This is because the wagon's motion was horizontal. Hence, we conclude that the relativistic effect of length contraction is observed only in the moving direction.
Another thing to point out here is the shape of objects during a relativistic event. Thus, any object in such an event still looks in the original shape despite the "pressing" effect caused by the motion at very high speed.
Example 3
What is the length of the wagon discussed in the theory section measured from a fixed point outside the wagon, if the wagon is moving at 0.8 c and the light signal needs 0.02 s to move from the source to the mirror and back to the source again when the event is viewed from inside the wagon? (The values may not be very realistic; they are only for illustration purpose.)
Solution 3
We have the following clues:
V = 0.8 c
Δt' = 0.02 s
L = ?
First, we work out the length L' of wagon in the system S' connected to the wagon. We have
L' = c ∙ ∆t'/2
= (3×108 m/s) ∙ (0.02 s)/2
= 3×106 m
Thus, the length L of wagon measured from outside it, is
= L' · √1 - (0.8 c)2/c2
= L' · √1 - 0.64
= L' · √0.36
= L' · 0.6
= 0.6 ∙ 3×106 m
= 1.8×106 m
You have reached the end of Physics lesson 18.3.3 Dilation of Time and Contraction of Length. There are 3 lessons in this physics tutorial covering Space and Time in Einstein Theory of Relativity, you can access all the lessons from this tutorial below.
More Space and Time in Einstein Theory of Relativity Lessons and Learning Resources
Whats next?
Enjoy the "Dilation of Time and Contraction of Length" physics lesson? People who liked the "Space and Time in Einstein Theory of Relativity lesson found the following resources useful:
- Dilation Of Time Feedback. Helps other - Leave a rating for this dilation of time (see below)
- Relativity Physics tutorial: Space and Time in Einstein Theory of Relativity. Read the Space and Time in Einstein Theory of Relativity physics tutorial and build your physics knowledge of Relativity
- Relativity Revision Notes: Space and Time in Einstein Theory of Relativity. Print the notes so you can revise the key points covered in the physics tutorial for Space and Time in Einstein Theory of Relativity
- Relativity Practice Questions: Space and Time in Einstein Theory of Relativity. Test and improve your knowledge of Space and Time in Einstein Theory of Relativity with example questins and answers
- Check your calculations for Relativity questions with our excellent Relativity calculators which contain full equations and calculations clearly displayed line by line. See the Relativity Calculators by iCalculator™ below.
- Continuing learning relativity - read our next physics tutorial: Relativistic Transformation of Velocity and the Relativistic Doppler Effect
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Space and Time in Einstein Theory of Relativity" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.
Relativity Calculators by iCalculator™
- Energy Calculator In Relativistic Events
- Frequency Calculator During Doppler Effect In Relativistic Events
- Length Calculator In Relativistic Events
- Lorentz Transformation Of Coordinates Calculator
- Lorentz Transformation Of Velocity Calculator
- Mass And Impulse Calculator In Relativistic Events
- Time Calculator In Relativistic Events
- Velocity Calculator In Relativistic Events