Menu
Physics Lesson 12.4.3 - Young's Double-Slit Experiment
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Young's Double-Slit Experiment, this is the third lesson of our suite of physics lessons covering the topic of Interference and Diffraction of Light, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Young's Double-Slit Experiment
The famous scientist Thomas Young developed a technique that is similar to the one described above to calculate the wavelength of a light wave. The only difference is that Young used two slits instead of a single slit to produce interference on the screen through diffraction of light waves. The reason for this decision was because it is very difficult to find point sources to produce light. It is much easier to use a large source such as a lamp or the Sun than a point source with very small dimensions. The two small slits are very close to each other, so the rays coming from the common source are coherent. As a result, the bright and dark fringes produced on the screen are more visible.
If the slits are circular, bright and dark circular fringes are produced on the screen and when slits are linear, bright and dark linear fringes are obtained. The only difference with the single slit diffraction lies in the circular slits, as unlike in the single slit diffraction a net of circular fringes is obtained in the Young Double slit experiment.
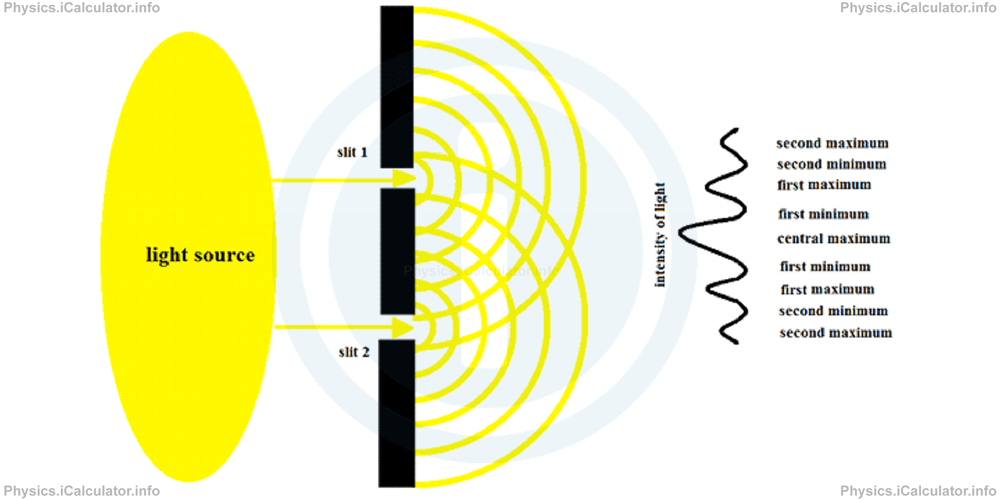
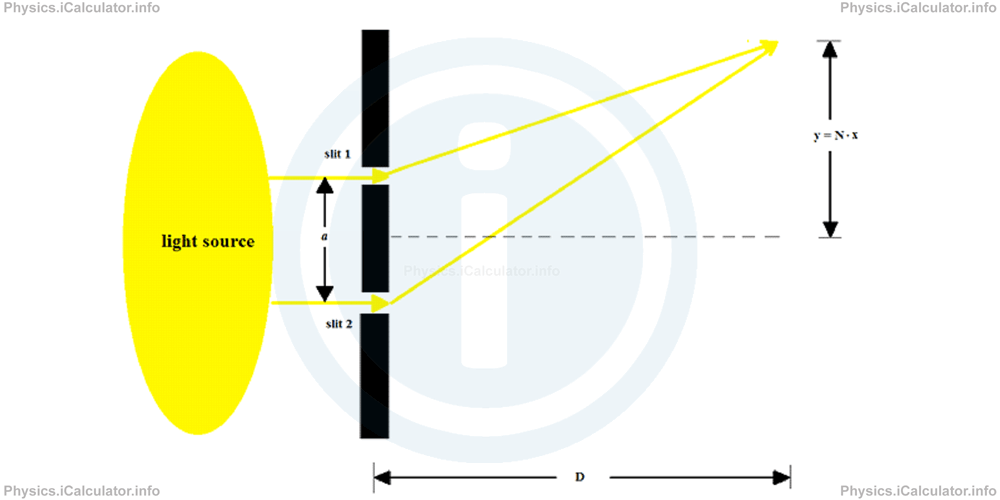
To determine the wavelength λ of the two coherent light waves passing through the slits, we must know three quantities:
- The distance (separation) between the two slits, a
- The distance (separation) between two fringes, i.e. the distance between the centres of two adjacent bright (or dark) regions, x and
- The distance from the slits to the screen, D.
Thus, the wavelength λ is calculated by the equation
The above equation is obtained by applying the triangles' similarity rules discussed earlier.
Example 2
Two coherent yellow light rays of wavelength 580 nm produced by the same source are incident in parallel through two thin slits of separation equal to 0.2 mm. What is the distance from the central maximum in which the seventh maximum is observed, if the screen is 4 m away from the slits? Take the figure above as a reference.
Solution 2
In this problem, we have the following clues:
a = 0.2 mm = 2 × 10-4 m
N = 7
D = 4 m
y = ?
First, the equation of Young's Double Slit Experiment is applied to calculate the separation x between two adjacent fringes. We have
x = λ × D/a
= 5.8 × 10-7 × 4/2 × 10-4
= 1.16 × 10-2 m
= 1.16 cm
Therefore, the 7th maximum is displaced by
= 7 × 1.16 cm
= 8.12 cm
in either direction (up or down) from the central maximum.
You have reached the end of Physics lesson 12.4.3 Young's Double-Slit Experiment. There are 4 lessons in this physics tutorial covering Interference and Diffraction of Light, you can access all the lessons from this tutorial below.
More Interference and Diffraction of Light Lessons and Learning Resources
Whats next?
Enjoy the "Young's Double-Slit Experiment" physics lesson? People who liked the "Interference and Diffraction of Light lesson found the following resources useful:
- Young Feedback. Helps other - Leave a rating for this young (see below)
- Optics Physics tutorial: Interference and Diffraction of Light. Read the Interference and Diffraction of Light physics tutorial and build your physics knowledge of Optics
- Optics Revision Notes: Interference and Diffraction of Light. Print the notes so you can revise the key points covered in the physics tutorial for Interference and Diffraction of Light
- Optics Practice Questions: Interference and Diffraction of Light. Test and improve your knowledge of Interference and Diffraction of Light with example questins and answers
- Check your calculations for Optics questions with our excellent Optics calculators which contain full equations and calculations clearly displayed line by line. See the Optics Calculators by iCalculator™ below.
- Continuing learning optics - read our next physics tutorial: Dispersion of Light
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Interference and Diffraction of Light" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.